Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.2 - Ex. 5

Encontre a derivada e enuncie a fórmula de integração correspondente.

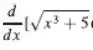
Passo 1

Galerinha, de boa? Pra esse exercício precisamos lembrar um pouco da parte de derivadas para nos ajudar a começar a resolver. Nisso, o essencial vai ser saber os métodos de derivação pra calcular cada caso e, pra isso, pega uma tabelinha ou uma lista de derivadas e vamos começar!!

Passo 2

Então, primeiro precisamos saber qual método de derivação é adequado pra calcular o que é dado. Como dentro da raiz quadrada há um termo dependente de x que á variável de interesse na derivação, podemos usar a derivação pela regra da cadeira que é dada por:

F ' x = f ' g x ∙ g ' x

Então, a partir da função inicial dada, vamos definir:

f u = u e g x = x 3 + 5

Precisamos encontrar a derivada de cada uma delas para substituir na equação da regra da cadeia. Portanto:

f ' u = 1 2 u → f ' g x = 1 2 x 3 + 5

E

g ' x = 3 x 2

Logo:

d d x x 3 + 5 = 1 2 x 3 + 5 ∙ 3 x 2 = 3 x 2 2 x 3 + 5

Passo 3

Encontrado o resultado da derivação, sabemos que a integral indefinida é como o caminho “inverso” ao da derivada (dito antiderivada). Pelo Teorema no item 5.2 . 2 (na página 323 do livro CÁLCULO VOL. 1 - 10ª ED - ANTON), temos que essa integral indefinida de uma função f x em um intervalo aberto pode ser dada pela fórmula geral:

∫ f x d x = F x + C

Onde C é uma constante arbitrária.

Então, integrando esse último resultado, teremos a forma geral da antiderivada da função dada por:

∫ 3 x 2 2 x 3 + 5 d x = x 3 + 5 1 / 2   + C

Resposta

d d x x 3 + 5 = 3 x 2 2 x 3 + 5

∫ 3 x 2 2 x 3 + 5 d x = x 3 + 5 1 / 2 + C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule as integrais fazendo a substituição u apropriada e aplicando as fórmulas revisadas nesta seção. ∫ sin ⁡ 3 x 2 + cos ⁡ 3 x d x
Calcule as integrais fazendo a substituição u apropriada e aplicando as fórmulas revisadas nesta seção. ∫ 1 9 + 4 x 2 d x
Calcule as integrais fazendo a substituição u apropriada e aplicando as fórmulas revisadas nesta seção. ∫ 4 x tan ⁡ ( x 2 ) d x
2-Uma bola é chutada para cima em um plano inclinado e volta à posição inicial depois de 4s. Se a distância total percorrida pela bola for de 16m, esboce a curva de velocidade versus tempo da bola.
4. A figura a seguir mostra a curva velocidade versus tempo no intervalo 1≤t≤5 de uma partícula quese move ao longo de um eixo horizontal. (a) O que pode ser dito sobre o sinal de aceleração naquele i