Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.5 - Ex. 9
Encontre as dimensões do retângulo com área máxima que pode ser inscrito em um círculo com raio de 10 cm
Passo 1
Uma imagem pode nos ajudar a raciocinar melhor sobre qual é a nossa situação:
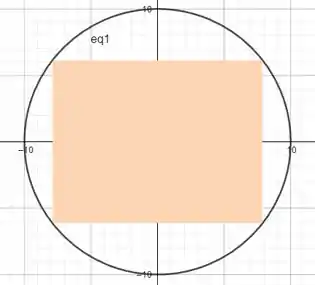
Esse é um típico exercício de otimização. O cálculo diferencial é uma ferramenta que nos ajuda muito na resolução desses casos, tão recorrentes no dia a dia.
Nesse caso, queremos inserir um retângulo com a maior área possível dentro dessa círculo, de raio igual a .
Passo 2
Agora, temos que a área do retângulo é dada pelo produto dos seus lados. Vamos assumir que seja a base e a altura. Teremos:
Nisso, precisamos escrever a área desse retângulo em função apenas de uma variável. No caso, vamos buscar escrever apenas em função de , pra termos uma .
Como correlacionamos e então?
Bom, nesse caso, a gente tem que a diagonal do retângulo equivale a dois raios do círculo de comprimento. Logo, a diagonal mede .
Por Pitágoras podemos correlacionar a base e a altura pela seguinte expressão:
Isolamos e teremos:
Agora, pegamos essa expressão pra e substituímos na equação pra área do círculo. Teremos:
Passo 3
Agora temos uma função que descreve a nossa área.
Queremos o ponto de máximo, que vai nos dar a maior área. E como fazer isso?
Se você ainda não sabe, ou talvez não lembre, mas um dos teoremas do Cálculo (Teorema de Fermat) diz que, nos pontos de máximo e de mínimo de uma função (quando possui) a derivada se anula.
Logo, podemos pegar , derivar e igualar a zero! Os valores de que acharmos atribuídos a essa derivada nula vão ser os pontos de máximo e mínimo.
Nisso, cabe a nós distinguir qual é qual, aplicando esses valores na função original e verificando qual nos dá o maior valor. Vai ser esse o nosso ponto de máximo!
Passo 4
Derivando, temos:
Igualamos isso a zero:
Dentre e , o que nos dá o ponto de máximo é , pois faz com que seja positivo, e valha seu maior valor.
Então, a base do retângulo deve medir pra que tenhamos a maior área possível.
E a altura? Calculamos pela expressão pra que já temos:
Ou seja, no fim das contas e têm o mesmo comprimento, que faz com que o retângulo seja, na verdade, um quadrado!
Resposta
As dimensões são .