Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.1 - Ex. 12
a) Esboce o gráfico de uma função em que tenha máximo absoluto, mas não tenha máximo local.
b) Esboce o gráfico de uma função em que tenha um máximo local, mas não tenha máximo absoluto.
Passo 1
E aí, tudo bem?! Essa é uma questão que trabalha a diferença entre máximo global e máximo local. No item (a), precisamos de uma função que tenha máximo global, mas não local; no item (b) queremos o oposto.
Vamos começar com o item (a):
Como queremos uma função que tenha máximo absoluto num intervalo fechado mas não tenham máximo local, vamos desenhar uma função estritamente nesse intervalo:
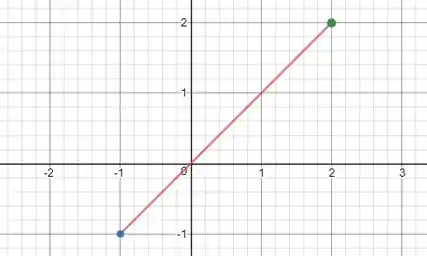
O máximo global ocorre em .
Passo 2
Item (b):
Queremos que a função tenha um máximo local mas não tenha máximo global: para isso podemos fazer a função explodir para de forma que ela não admita máximo global.
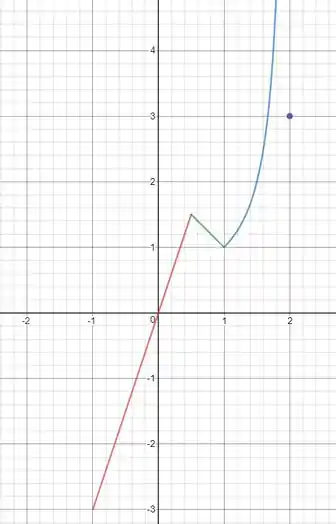
Note que a função tem um máximo local, porém ela explode quando . Além disso, observe que definimos ela em com para que ela esteja definida no intervalo todo.
Resposta
Esboço de gráfico.