a) Esboce o gráfico de uma função em que tenha um máximo absoluto, mas não tenha mínimo absoluto.

b) Esboce o gráfico de uma função em que seja descontínua, mas tenha tanto máximo absoluto como mínimo absoluto.

Vamos fazer primeiro o item (a).

Como não queremos que a função tenha mínimo absoluto, basta fazermos ela explodir para .

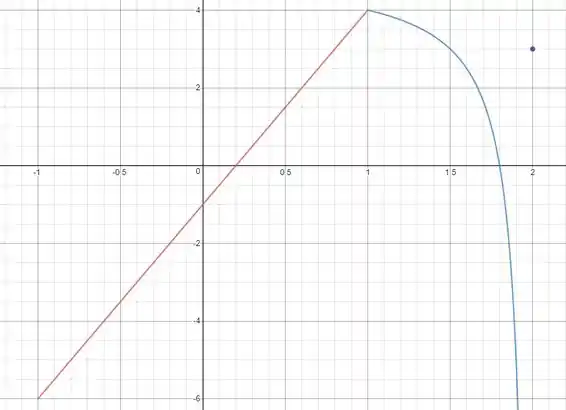
Note que fizemos para que a função esteja definida em todo intervalo.

Agora vamos resolver o item (b).

Queremos uma função que tenha os dois extremos globais, mas seja descontínua. Um exemplo:

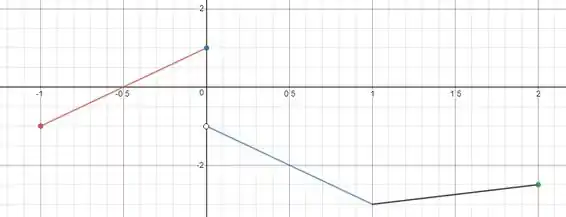
O máximo ocorre em e mínimo em . Ela é dexontínua em .