Encontre as dimensões do retângulo com a maior área que pode ser inscrito em um triângulo equilátero com lado se um dos lados do retângulo estiver sobre a base do triângulo.
Passo 1
O exercício quer os valores máximos que a largura e a altura de um retângulo, que chamaremos respectivamente de e , podem assumir dada a restrição imposta pelo tamanho do triângulo equilátero de lado . Primeiro esboçamos uma figura hipotética:
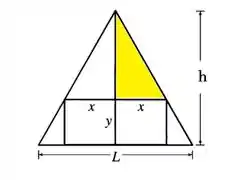
Passo 2
Para encontrarmos as dimensões pedidas, utilizaremos semelhança de triângulos, comparando o triângulo retângulo de altura e , com o triângulo menor preenchido de amarelo,
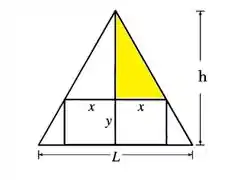
formando a seguinte equação:
Temos a fórmula dependendo de muitas variáveis, então vamos fazer a altura depender de usando Pitágoras:
Isolando a altura, teremos:
E fazendo o quadrado de , teremos:
Agora vamos tirar o mmc entre os denominadores e subtrair as frações. Assim, ficamos com:
E para deixar sozinha, basta tirar a raiz quadrada dos dois lados da equação, assim:
Passo 3
Agora vamos substituir essa altura na fórmula de semelhança para isolarmos mais uma variável e tornar a equação possível de resolver:
Sendo
Substituindo, ficamos com:
Agora vamos multiplicar cruzado tudo isso aí:
Podemos cortar dos dois lados da equação, e teremos:
E isolando , ficamos com:
Ou melhor, colocando em evidência:
Passo 4
Agora vamos pensar no que a gente está procurando. Queremos as dimensões do retângulo com a maior área. E a área de um retângulo
Substituir na fórmula da área, ficamos com:
E fazendo a distributiva, ficamos com:
Passo 5
Como queremos a maior área, vamos maximizar , derivando sua expressão e igualando a zero.
Sendo
Sua derivada será:
Igualando a zero, ficamos com:
E resolvendo temos:
E isolando o , ficamos com:
Substituindo em :
E essas são as dimensões do maior retângulo possível.
Resposta
Largura do retângulo:
Altura do retângulo: