Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 1.1 - Ex. 37
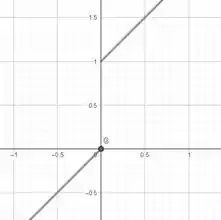
Encontre o domínio e esboce o gráfico da função
Passo 1
Opa, bora lá! A questão nos pede para encontrar o domínio da função, ou seja, quais valores de nós temos na função de tal forma que ela exista e, além disso, pede para que plotemos o gráfico dessa função:
Analisando o domínio da função percebemos que podemos colocar qualquer valor real na função que não vai dar nenhum problema, logo o domínio da nossa função são todos os reais ou:
Passo 2
Agora a gente plota o gráfico da função. Temos dois seguimentos de retas, assim:
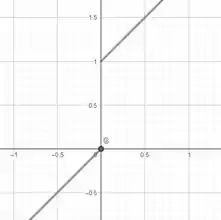
Prontinho!
Resposta
Exercícios de Livros Relacionados
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.O gráfico de uma função par é simétrico em relação ao eixo y .
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.O gráfico de y = f x + 2 + 3 é obtido transladando o gráfico de y = f ( x ) duas unidades para a direita e três para cima.
Use a tabela do exercício 47 para resolver as equações f g x = 0 e g f x = 0
Encontre(f (x + h) - f ( x ))/(h) E(f (w) - f ( x ))/(w - x) E simplifique tanto quanto possível.f (x) = 3 x^2 - 5
Encontre f x + h - f ( x ) h E f w - f ( x ) w - x E simplifique tanto quanto possível. f x = x 2 + 6 x