Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.2 - Ex. 52
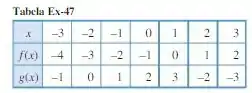
Use a tabela do exercício 47 para resolver as equações e
Passo 1
No exercício 47, achamos e :
Além disso, também achamos ;
Que tinha esse gráfico:
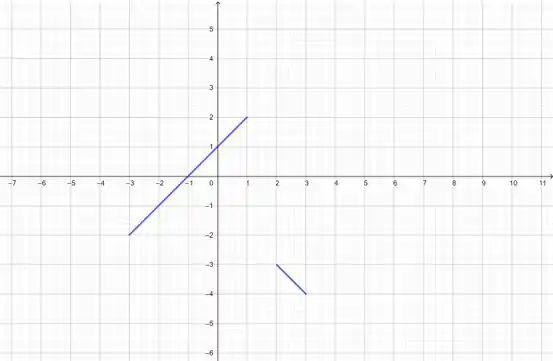
E, olhando para ele, podemos ver que a solução de está, mais ou menos, em .
Que é onde a função toca o eixo .
Passo 2
Para achar a solução de , vamos, primeiro, achar essa função e buscar no gráfico dela onde ela toca o eixo .
Para achar , precisamos substituir de pela função . Então, como é dada por partes, essas substituições também serão por partes:
Para , . Substituindo :
Para , . Substituindo :
Juntando essas informações, podemos definir a composição como:
Vamos jogar isso em um gráfico:
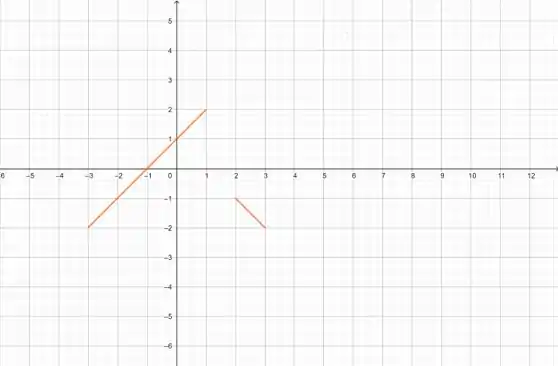
E, olhando para ele, podemos ver que a solução de está, mais ou menos, em .
Que é onde a função toca o eixo .
Prontinho!
Resposta
Ambas as soluções estão em .