Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 1.1 - Ex. 37
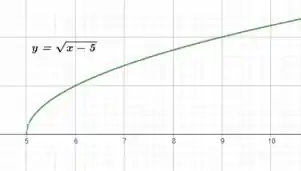
Encontre o domínio e esboce o gráfico da função:
Passo 1
Fala aí, pessoal!
Nesse problema foi dada a função
E nosso objetivo é determinar o domínio dessa função e esboçar seu gráfico.
Parece complicado?
Podemos definir o domínio de uma função como sendo os possíveis valores que a variavel pode assumir para que a função exista.
Então vamos analisar a estrutura da função e definir esses valores.
Já para esboçar o gráfico da função vamos obsrevar algumas características da função.
Veja só!
Passo 2
Como nossa função é dada por
Perceba que nossa função é uma raiz e como bem sabemos, não existe raiz de valores negativos...
Isso significa que para existir o conteúdo dentro da sua raiz deve ser
Portanto, para existir, ... escrevendo isso matematicamente, temos
Tranquilo até aqui?
Passo 3
Agora bora desenhar o gráfico!
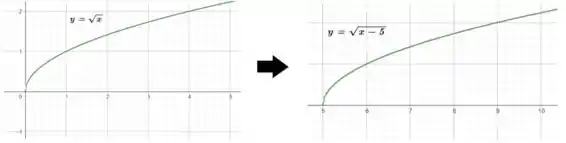
Sabemos como é o gráfico de , não é?
Perceba que nesse caso temos um deslocamento no eixo .
Então o gráfico de será igual a porem deslocado unidades para a direita.
E aí! entendeu tudo? Responde Aí!
Resposta
