Encontre o domínio e a imagem e esboce o gráfico da função .
Passo 1
Eaee, belezinha??

Bom... a questão nos dá a seguinte função:
Queremos encontrar o domínio, a imagem e o esboço do gráfico dessa função.
Para isso, temos que entender alguns conceitos:
- O domínio de uma função é o conjunto de todos os valores de entrada para os quais a função é definida;
- A imagem de uma função é o conjunto de todos os valores de saída que a função pode produzir quando aplicada aos elementos do domínio.
Assim, para resolver essa questão, a primeira coisa que devemos encontrar é o domínio da função!!
E aí?? Bora lá?? 😉
Passo 2
Como temos uma função raiz quadrada, sabemos que o que tem dentro da raíz não pode ser um número negativo!
Logo, podemos escrever uma inequação que representa isso dessa forma:
Agora, passamos o para o outro lado:
Multplicando tudo por (não esquece que o sinal do meio muda de lado quando fazemos isso!):
Agora, temos que lembrar de uma igualdade muito importante quando a gente trabalha com uma inequação!
É a propriedade que diz para a gente que .
Isso é importante porque essa alteração na inequação vai fazer a gente visualizar melhor o domínio no final das contas. Dá uma olhada:
Jogando a raiz para o outro lado:
Toda vez que a gente tem um módulo assim na inequação, a gente pode “abrir” ele ficando da seguinte forma:
Sacou? A gente tira o módulo e põe o valor negativo do outro lado, desse jeito que ta aí, sem mistério!
Esse vai ser o nosso domínio então, que podemos escrever na forma do intervalo .
Tranquilo até aqui? 😉
Passo 3
Agora, iremos achar a imagem da nossa função.
Qual é o menor valor que pode assumir? Vai ser justamente quando , veja:
O mesmo vale para , já que , Tranquilo?
Agora vamos pensar qual o maior valor que pode assumir, levando em conta o domínio da nossa função.
Isso vai acontecer quando , pois aí não vamos ter nenhum valor sendo subtraído do , sacou? Nesse caso, vai acontecer o seguinte:
Então vai ser o maior valor possível para a nossa imagem.
Daí a gente consegue tirar que a nossa imagem vai ficar, então, no intervalo .
Legal, né? 😉
Passo 4
Por fim, falta só desenhar o gráfico da questão!
Você pode tentar desenhar vários pontos dessa curva para montar o gráfico, mas tem um certo “atalho” que, sabendo, você já consegue dizer de cara o gráfico dessa função!
Primeiro, vamos chamar de , ou seja, . A gente pode, então, fazer o seguinte para dar uma arrumada na expressão que temos:
Conseguiu reconhecer? Essa daí é a expressão de uma circunferência centrada na origem, lá da geometria! Daí, a gente tira que o raio dessa circunferência é .
Acontece que a nossa expressão representa a parte superior de uma circunferência de raio , sacou?
A parte inferior seria dada por uma outra função, uma por exemplo, que seria da forma . Então toda vez que você ver função assim com raíz quadrada, vai logo suspeitando!
Sabendo disso, o gráfico da nossa função, então, vai ficar assim:
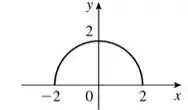
Entendeu direitinho?? Responde Aí! 😉
Resposta
O domínio fica no intervalo , a imagem no intervalo e o gráfico da função vai ser a parte superior de um círculo de raio centrado na origem: