Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.8 - Ex. 2
(a) Encontre de em
(b) Encontre um ponto em tal que .
(c) Esboce o gráfico de em e construa um retângulo acima do intervalo cuja área seja igual à área abaixo do gráfico de naquele intervalo.
Passo 1
(a) Para calcular o que ele pede é só usar a fórmulinha:
Passo 2
(b) Descobrimos que
Queremos achar um valor de que resulte em . Podemos escrever:
Como a gente quer o valor de dentro do intervalo :
Passo 3
(c) Só desenhar o gráfico de em , e um retângulo que tem o mesmo comprimento que o intervalo e altura , já que:
Fica assim:
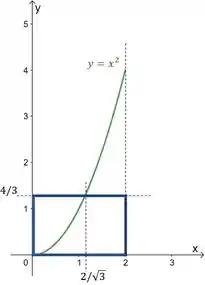
Resposta
(a)
(b)
(c) 
Exercícios de Livros Relacionados
26. O seguinte teorema é uma generalização do Teorema do valor médio para integrais: se f e g forem contínuas no intervalo fechado [ a , b ] e g x0 para todo x no intervalo aberto ( a , b ) , então ex
Suponha que f x0 e contínua em um intervalo [a,b]. Prove que ∫ a b f x d x0
Suponha f x0 e contínua em[a,b]. Prove que se ∫ a b f x d x = 0 , então f x = 0 , para todo x ∈ [ a , b ]
Se f x = x + 2 x - 3 , ache a média dos valores de f no intervalo 4,6 .
Se f x = 1 x , ache a média dos valores de f no intervalo 1,5 .