Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.3 - Ex. 25
Determine o volume do sólido dado.
25.
Abaixo da superfície e acima do triângulo com vértices , e
Passo 1
Tudo show, gente bonita?
Olha só, segundo a questão, precisamos encontrar o volume do sólido que está abaixo da superfície e acima do triângulo cujos vértices ele nos deu.
Primeiramente vamos analisar a região :
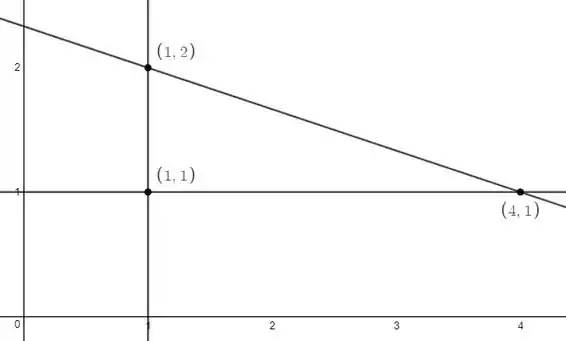
Podemos representar essa área como sendo do tipo I ou II, ou seja, a região faz “sombra” no eixo ou no eixo .
Vou escolher essa região como Tipo I, portanto faz “sombra” em .
Asism, já descobrimos os limites de integração nesse eixo:
Para definir os limites de integração de , a única dificuldade que teremos é achar a reta que passa entre e .
A inclinação da reta pode ser definida por essa fórmula:
Substituindo pelos valores que já temos:
Então, podemos escrever da seguinte forma
Passo 2
Temos, então que o volume do solido que é restrito abaixo de na região é dado por
Agora vamos trabalhar com a integral de dentro, ou seja, integrar primeiro em :
Substituindo os limites de integração em , teremos:
Como os denominadores estão diferentes, realizando o M.M.C.:
Agora integrando em relação a , vamos fazer a mágica acontecer!
Podemos colocar a fração para fora da integral como se fosse uma constante, assim: