Os Exercícios 1-18 fornecem equações paramétricas e intervalos de parâmetro para o movimento de uma partícula no plano . Identifique a trajetória da partícula encontrando a equação cartesiana para ela. Desenhe o gráfico de cartesiana (os gráficos irão variar conforme a equação utilizada). Indique a parte do gráfico percorrida pela partícula e a direção do movimento.
13.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
No início da tarefa, vamos observar que a variável pode assumir valores entre e (porque a variável é igual ao parâmetro ), ou seja,
Como o parâmetro é igual a , então se incluirmos na equação que contém , obtemos:
A raiz quadrada é uma função não negativa. Portanto, devido a , concluímos que . Para facilitar o desenho da equação cartesiana, vamos elevar ao quadrado a expressão (1):
Com isso, nós temos que
Como é não negativo , vamos desenhar a parte do círculo acima do eixo .
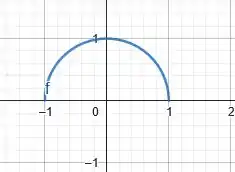
Como assume valores dentro do intervalo , então também assume valores dentro desse mesmo intervalo. Portanto, concluímos que pode assumir apenas valores negativos.
Passo 2
Se desenharmos esses pontos no círculo, obtemos a direção do movimento da partícula:
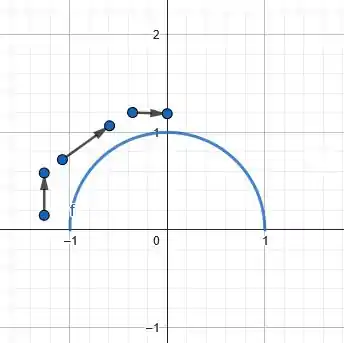
Determinamos a direção do movimento da partícula para que as setas passassem de valores menores do parâmetro para valores maiores.