Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.1 - Ex. 12
Os Exercícios 1-18 fornecem equações paramétricas e intervalos de parâmetro para o movimento de uma partícula no plano . Identifique a trajetória da partícula encontrando a equação cartesiana para ela. Desenhe o gráfico de cartesiana (os gráficos irão variar conforme a equação utilizada). Indique a parte do gráfico percorrida pela partícula e a direção do movimento.
12.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
No início da tarefa, nosso objetivo é escrever como uma função que depende de , ou seja, temos que eliminar o parâmetro . Para poder escrever como uma função que depende de , vamos expressar o parâmetro da variável .
Desenvolvendo um pouco mais os termos
Isolando o
Se nós colocarmos o valor de na expressão de , obtemos que
Com isso, já podemos desenhar a curva!
Passo 2
Se plotarmos os pontos no sistema de coordenadas, obtemos a seguinte função racional:
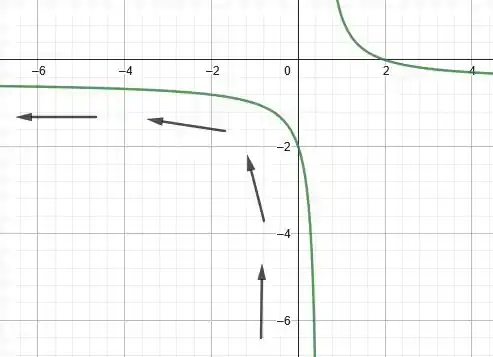
Pelas condições do problema, sabemos que pode assumir valores dentro do intervalo . Podemos escrever a variável em função do parâmetro como:
Como , então a desigualdade se torna
Obtemos que a variável x pode assumir valores dentro do intervalo:
Passo 3
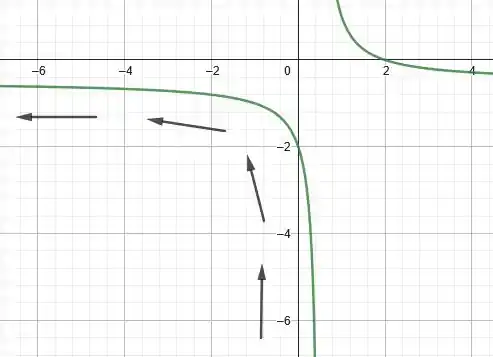
Concluímos que desenhamos o gráfico da função racional no intervalo . Na primeira figura, vamos marcar a parte da função que satisfaz a condição de que x é menor que . Se desenharmos esses pontos na função racional, obtemos a direção do movimento da partícula:
