Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.1 - Ex. 18
Os Exercícios 1-18 fornecem equações paramétricas e intervalos de parâmetro para o movimento de uma partícula no plano . Identifique a trajetória da partícula encontrando a equação cartesiana para ela. Desenhe o gráfico de cartesiana (os gráficos irão variar conforme a equação utilizada). Indique a parte do gráfico percorrida pela partícula e a direção do movimento.
18.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Como , o que pode ser escrita como , com isso, a equação cartesiana é igual a
O que pode ser escrito como
Pelo gráfico, nós temos que
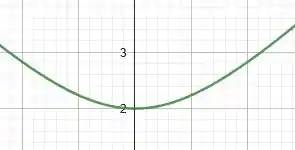
Resposta
Respondido acima!
Exercícios de Livros Relacionados
Ligue as equações paramétricas aos gráfico de I-VI. x = cos t , y = s e n( t + s e n5 t )
Ligue as equações paramétricas aos gráficos de I-VI. x = t 3 - 1 , y = 2 - t 2
Ligue as equações paramétricas aos gráfico de I-VI. x = s e n t + s e nt , y = c o s ( t + cos t )
Ligue as equações paramétricas aos gráficos de I-VI. x = t 3 - 2 t , y = t 2 - t
Mostre que a curva polar r = 4 + 2 sec θ (chamada conchóide) tem a reta x = 2 como uma assíntota vertical mostrando que no limite lim r → ± ∞ x = 2 . Use esse fato para ajudar a esboçar a conchóid