Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.1 - Ex. 15
Os Exercícios 1-18 fornecem equações paramétricas e intervalos de parâmetro para o movimento de uma partícula no plano . Identifique a trajetória da partícula encontrando a equação cartesiana para ela. Desenhe o gráfico de cartesiana (os gráficos irão variar conforme a equação utilizada). Indique a parte do gráfico percorrida pela partícula e a direção do movimento.
15.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
No início da tarefa, vamos escrever a equação paramétrica em coordenadas cartesianas.
Para fazer isso, temos que eliminar o parâmetro . Qual é a conexão entre a função secante e a função tangente?
Como a função secante é um cosseno recíproco, então:
Como a variável é definida como , então usando a expressão (1) concluímos que podemos escrever a variável x também como:
Como é igual à função tangente, podemos escrever a expressão (2) como:
Passo 2
O gráfico da equação anterior é uma parábola voltada para o eixo . No intervalo , a função tangente toma todos os números reais. Portanto, tem todo o conjunto de números reais para a imagem. Como é definido como , devido ao quadrado, assume todos os números não negativos. Dadas as conclusões anteriores, desenhamos a parábola inteira ou apenas uma pequena parte?
Como a imagem de é o conjunto completo de números reais, desenhamos a parábola inteira (porque incluímos qualquer valor de na equação da parábola).
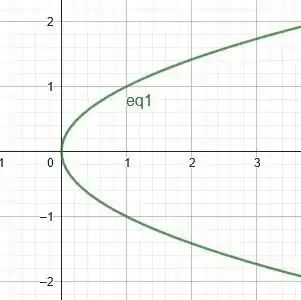
As coordenadas da posição da partícula satisfazem a equação , então a partícula se move ao longo da parábola .
Passo 3
Se desenharmos esses pontos na parábola, obtemos a direção do movimento da partícula:
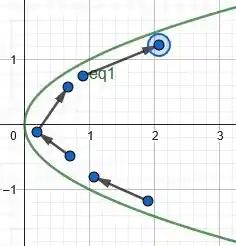
Determinamos a direção do movimento da partícula para que as setas passassem de valores menores do parâmetro t para valores maiores.