Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.7 - Ex. 38
Encontre uma equação da reta tangente à curva em cada um dos pontos dados. Faça um esboço do gráfico e inclua segmento de retas tangentes nos pontos dados.
Passo 1
A questão pede para encontrarmos a equação da reta tangente à curva em diversos pontos. Vale lembrar que a equação da reta tangente que passa por um ponto é dada por
Assim, vamos encontrar primeiro :
Passo 2
Para o ponto , temos que
Assim, a equação da reta será
Portanto,
Ilustramos isso na figura a seguir:
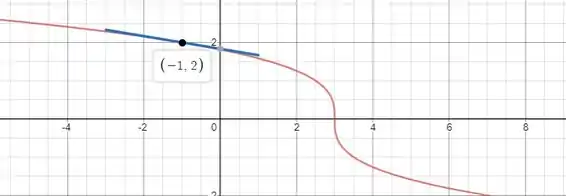
Passo 3
Já para o ponto , temos que
Assim,
A reta tangente é mostrada na figura:
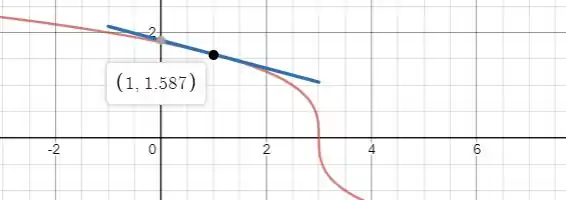
Passo 4
Note que para o denominador da derivada se anula, isto é, a função não é derivável nesse ponto e sendo assim, não admite reta tangente.
Já para o ponto , temos que
Assim,
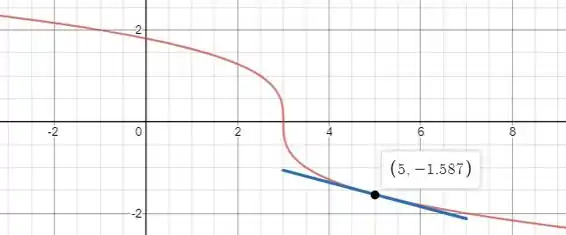
Passo 5
Por fim, no ponto , temos que
Assim,
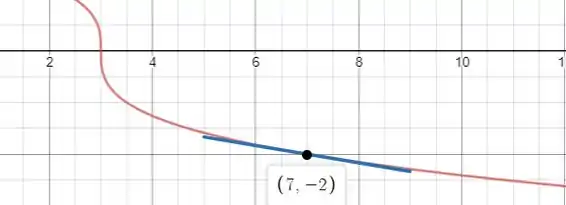
Resposta
Esboço de gráficos.
Exercícios de Livros Relacionados
Um tanque com capacidade para 1000 galões de água é drenado pela base em meia hora. Os valores na tabela mostram o volume V de água remanescente no tanque (em galões) após t minutos. Se P for o ponto
Uma flecha é lançada para cima com uma velocidade de 58m / s , e sua altura em metros após t segundos é dada por h = 58 t - 0,83 t 2 .Encontre a velocidade média durante os intervalos de tempo dados:E
O ponto P 2 , ln 2 pertencente à curva y = ln x . Se Q é o ponto ( x , ln x ) , use a sua calculadora para determinar o coeficiente da reta secante P Q , com precisão de seis casas decimais, par
O deslocamento (em pés) de uma certa partícula movendo-se em linha reta é dado por s = t 3 6 .Encontre a velocidade média durante os períodos de tempo a seguir:Encontre a velocidade instantânea quando
A inclinação da reta tangente ao gráfico da função exponencial y = 2 x no ponto ( 0,1 ) e lim x → 0 ( 2 x - 1 ) x . Estime a inclinação até três casas decimais.