Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.3 - Ex. 25
a) Encontre uma equação da reta tangente à curva no ponto .
b) Ilustre a a parte (a) fazendo o gráfico da curva e da reta tangente na mesma tela.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente encontrar a equação da reta tangente à curva no ponto .
Essa equação da reta é dada de forma geral por:
Onde é o ponto dado e é o coeficiente angular da reta.
Para encontrar esse coeficiente, precisamos derivar a função , usando a regra do produto, e substituir tudo na equação da reta.
Lembrando que a regra do produto é dada da seguinte forma:
Depois, vamos esboçar o gráfico da função e da reta tangente na mesma tela.
Vamos lá! 😉
Passo 2
Vamos começar derivando a nossa função para encontrar o coeficiente angular da reta tangente. Usando a regra do produto, temos:
Agora, vamos substituir e :
Como e , temos:
Passo 3
Então, usando , e na equação da reta, vamos ter:
Isolando :
E simplificando:
Essa é a equação da reta tangente à curva no ponto .
Passo 4
Esboçando a curva , em vermelho, a reta tangente , em azul, temos:
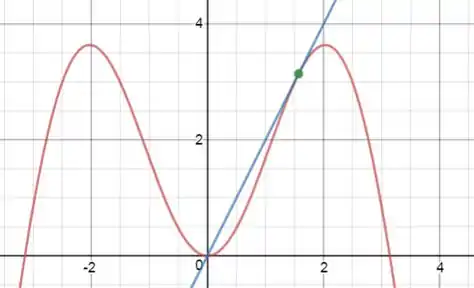
Valeu, galera! Até a próxima! 😉
Resposta
a) .
b) Esbcoço de gráfico.