Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.2 - Ex. 49
Se e forem funções cujos gráficos estão ilustrados, seja e .
a) Encontre .
b) Encontre .
Passo 1
E aí, galerinha? 😬
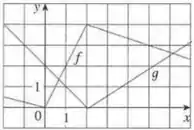
O enunciado nos deu o gráfico de duas funções e e definiu duas novas funções: sendo o produto de por e sendo o quociente de por .
A partir daí, devemos achar as derivadas dessas funções conhecendo as derivadas de e .
e
Parece complicado?
Para resolver esse problema temos que prestar atenção que consiste em um produto de funções, então sua derivada pode ser calculada a partir da regra do produto
Já a função consiste no quociente de duas funções, então sua derivada pode ser calculada a partir da regra do quociente...
Veja só! 😉
Passo 2
No item a) queremos a derivada de , ou seja
Vamos aplicar a regra do produto
Substituindo :
Analisando o gráfico, é imediato que e .
Como e são retas em torno de , suas derivadas nesse ponto serão os coeficientes angulares das retas.
Substituindo esses valores na expressão para :
Tranquilo até aqui? 😉
Passo 3
Agora no item b) queremos calcular a derivada de
Aplicando a regra do quociente:
Substituindo :
Note que do gráfico tiramos e . Além disso,
Assim,
E aí! o que achou? Responde Aí! 😊
Resposta
a) .
b) .