Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.2 - Ex. 31

Encontre uma equação da reta tangente à curva no ponto especificado.

31) y = x ² - 1 x ² + x + 1 ,     ( 1,0 )

Passo 1

Legal galera, a inclinação da reta tangente é obtida pela derivada da função, lembram?

m t g = y '

Então precisamos achar a derivada da função, mas como? Antes de tudo devemos notar que há uma divisão entre os termos. Então o que usamos?

A Regra do Quociente, certo? Vamos lembrar:

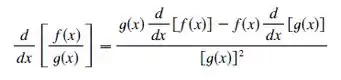
Passo 2

Se chamarmos:

f x = x ² - 1

g x = x ² + x + 1

Derivando:

d d x f x = 2 x

d d x g x = 2 x + 1

Substituindo:

d d x f x g x = x ² + x + 1 2 x - ( x ² - 1 ) ( 2 x + 1 ) ( x ² + x + 1 ) ²

Então:

d d x f x g x = y ' = x 2 + 4 x + 1 ( x ² + x + 1 ) ²

No ponto (1,0), iremos substituir os valores do ponto na nossa derivada:

y ' = 1 2 + 4.1 + 1 ( 1 ² + 1 + 1 ) ² = 6 3 2 = 2 3

Passo 3

Não é bem isso que queremos, não é? Sabemos que:

m t g = y ' = 2 3

Mas queremos a equação da reta tangente que passa por (1,0). Então vamos lembrar a equação da reta:

y - y p = m t g ( x - x p )

Onde y p   e   x p são os pontos pelo qual a reta passa.

Agora ficou fácil, é só substituir:

y - 0 = 2 3 ( x - 1 )

Então:

y = 2 3 x - 2 3

E acabamos!

Resposta

y = 2 3 x - 2 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a derivada da funçãov = (1 + x - 4 sqrt(x))/(x)
Determine a derivada da funçãoy = (x^2 + 3 e^x)/(2 e^x - x)
Determine a derivada da funçãou = (5 x + 1)/(2 sqrt(x))
Determine a derivada da funçãor = 2 ((1)/(sqrt(theta)) + sqrt(theta))
Determine a derivada da funçãoy = ((x + 1) (x + 2))/((x - 1) (x - 2))