Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.7 - Ex. 17
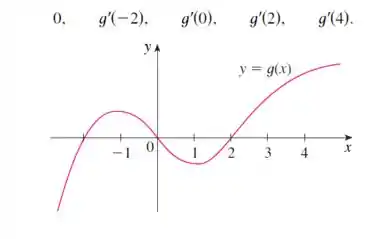
Para a função cujo gráfico é dado, arrume os seguintes números em ordem crescente e explique seu raciocínio
Passo 1
Opaaa, bora resolver esse problema!
O enunciado nos dá o seguinte gráfico:
A partir dele temos que organizar as seguintes números em ordem crescente:
, , , ,
Pra resolver essa questão precisamos lembrar que é a inclinação da reta tangente no ponto . Então nos próximos passos, vamos tentar visualizar e comparar as inclinações nos pontos dados.
Agora vamos colocar a mão na massa!
Passo 2
Vamos tentar destacar as inclinações nos pontos dados. Olha só:
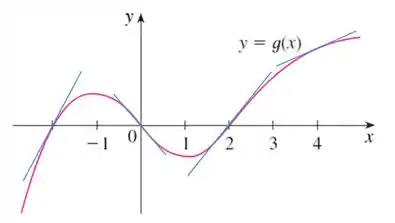
Veja bem. A primeira coisa que chama a atenção é que a inclinação em é decrescente, enquanto que as demais são crescentes. Quando essa inclinação é decrescente, podemos dizer que a derivada é negativa, enquanto que se a inclinação for crescente, a derivada é positiva.
Dessa forma, concluímos que
Então já sabemos que é o menor valor que estamos comparando. Vamos analisar os que faltam.
Passo 3
Beleza! A comparação é feita no olho mesmo. Basicamente, quanto mais perto da horizontal (deitada) a inclinação, menor é a derivada; e quanto mais perto da vertical (em pé), maior a derivada.
Vamos voltar a olhar pro nosso gráfico, mas agora focando apenas nos pontos onde é igual a e e :
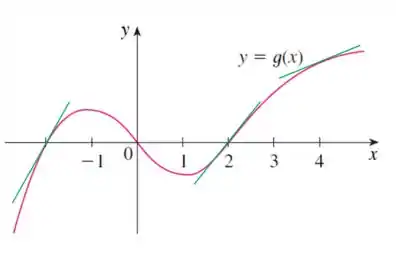
Pela nossa figura, aparentemente o ponto apresenta a inclinação mais deitada. Então seria a menor derivada.
Com relação aos pontos que restam parece que tem a inclinação mais em pé.Então seria a nossa maior derivada.
Então agora juntando todas as informações, temos que:
Prontinho! Entendeu tudo? Responde Aí! 😊