Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 16.6 - Ex. 9
Use um computador para traçar o gráfico da superfície paramétrica. Imprima o resultado e indique sobre ele quais são as curvas da grade que têm constante e quais tem constante.
Passo 1
Da parametrização dada, temos que
O gráfico completo da superfície é dado pelo domínio paramétrico . Observe que se for constante, as equações paramétricas se tornam,
e
representa um círculo de raio no plano .
Então, a grade circular curva horizontal são as curvas da grade que são constantes. As curvas da grade vertical, então, correspondem a sendo mantido constante, dando e com o qual tem um formato de “oito”.
Passo 2
O gráfico da superfície paramétrica é:
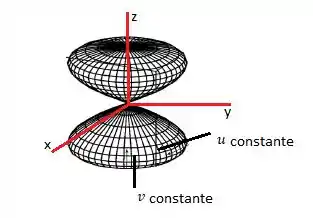
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Faça uma correspondência entre as equações e os gráficos identificados por I-VI e justifique sua resposta. Determine quais famílias de curvas da grade têm u constante e quais têm v constante. r u , v
Faça uma correspondência entre as equações e os gráficos identificados por I-VI e justifique sua resposta. Determine quais famílias de curvas da grade têm u constante e quais têm v constante. r u , v
Faça uma correspondência entre as equações e os gráficos identificados por I-VI e justifique sua resposta. Determine quais famílias de curvas da grade têm u constante e quais têm v constante. x = 1 -
Determine uma representação paramétrica para a superfície.A metade inferior do elipsoide 2 x 2 + 4 y 2 + z 2 = 1 .
Determine uma representação paramétrica para a superfície.O plano que passa pelo ponto 1,2 , - 3 e contém os vetores i + j - k e i - j + k .