Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 21

Encontre e esboce o domínio da função.

f x , y , z = 4 - x 2 + 9 - y 2 + 1 - z 2

Passo 1

Eaee, tudo tranquilinho?? Bom... o enunciado nos deu a seguinte função de duas variáveis:

f x , y , z = 4 - x 2 + 9 - y 2 + 1 - z 2

Queremos determinar o domínio de f x , y , z , ou seja, queremos saber que valores de x , y e z que podem ser usados para que f x , y , z seja real.

Para definir o domínio é melhor olhar para as retrições que possibilitam que a gente tenha uma solução real.

Em seguida, a gente vai plotar o nosso domínio!! 😉

Passo 2

Temos que:

f x , y , z = 4 - x 2 + 9 - y 2 + 1 - z 2

Temos três restrições aqui, uma para cada raiz (lembre-se que a raiz quadrada só funciona para um número positivo):

Na primeira:

4 - x 2 > 0 ∴

x 2 ≤ 4 ∴

- 2 ≤ x ≤ 2

Na segunda:

9 - y 2 > 0 ∴

y 2 ≤ 9 ∴

- 3 ≤ y ≤ 3

Na terceira:

1 - z 2 > 0 ∴

z 2 ≤ 1 ∴

- 1 ≤ z ≤ 1

Passo 3

Logo, o domínio é definido por:

D : { ( x , y , z ) | - 2 ≤ x ≤ 2 ,   - 3 ≤ y ≤ 3 ,   - 1 ≤ z ≤ 1 }  

Assim, plotando o domínio, temos:

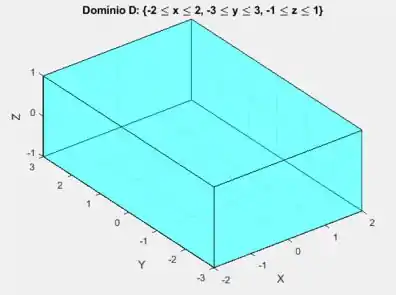
Resposta

D : { ( x , y , z ) | - 2 ≤ x ≤ 2 ,   - 3 ≤ y ≤ 3 ,   - 1 ≤ z ≤ 1 }

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma fina placa de metal, localizada no plano x y , tem a temperatura T x , y no ponto x , y . Desenhe algumas curvas de nível (isotermas) se a função de temperatura for dada por T x , y = 100 1 + x 2
Faça um esboço de um mapa de contorno e um gráfico da função e compare-os. f x , y = x 2 + 9 y 2