Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 52
Faça o mapa de contorno da função mostrando vérias curvas de nível.
Passo 1
Fala ai, tranquilo?
Nossa missão nesta questão é construir um mapa de contorno.
Vamos começar entendendo o que é um mapa de contorno? 😊
Um mapa de contorno é um gráfico que mostra curvas de níveis de uma função de duas variáveis. Cada cruva de nível conecta pontos no plano onde a função tem o mesmo valor. Isso nos proporciona uma representação visual das variações da função no plano, nos dando padrões e pontos críticos.
Para se desenhar o mapa de contorno, precisa-se chegar à função das curvas de nível.
Basta fazer e depois ir variando (dando valores) para representar algumas curvas de nível no mapa.
Em outras palavras, temos que verificar o comportamento da curva para diferentes valores.
Vamos começar?
Passo 2
ATENÇÃO:
Para , temos que
Essa é a função de um círculo:
com , e .
Ou seja, temos círculos centrados em e com raio igual a .
Passo 3
Vamos esboçar as curvas de nível para esses valores de :
Curva para
Essa é uma parábola, voltada para cima
Curva para
Essa é uma parábola, mas voltada para baixo.
Passo 4
Variando , chega-se ao seguinte mapa de contorno:
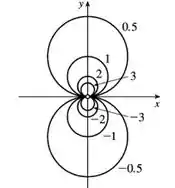
Vale notar o ponto em aberto no gráfico correspondente ao ponto
O mapa de contorno da função consiste em curvas que são parábolas abertas, voltadas para cima ou para baixo dependendo dos valores de . As curvas se aproximam do eixo para e se abrem conforme os valores de se afastam de zero.
Resposta
