Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 53
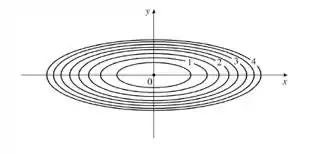
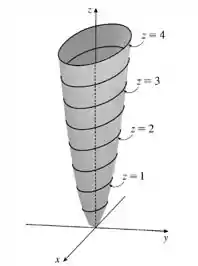
Faça um esboço de um mapa de contorno e um gráfico da função e compare-os.
Passo 1
Falaaaaaa, meu parceiro. Vamos resolver essa atividade marota aqui.
Veja bem, a gente quer desenhar o gráfico e o mapa do contorno da função:
Para se desenhar o mapa de contorno, precisa-se chegar à função das curvas de nível. Basta fazer e depois ir variando (dando valores) para representar algumas curvas de nível no mapa.
Para se desenhar o gráfico da função, basta fazer . Trata-se de uma superfície em .
Parece tudo muito simples, mas a gente precisa pensar um pouco. A curva de nível é uma planificação da função, quando fazemos a curva de nível, estamos visualizando a nossa função de cima, ela está ‘amassada’ no plano .
É interessante então, em muitos casos analisarmos se a equação da nossa função não é uma equação conhecida, uma elipse, uma circunferência, pois aí já saberemos mais ou menos como desenhar.
Mas mesmo que não seja, é importante que encontremos os pontos de intersecção da função com os eixos , fazemos isso escolhendo um valor para e zerando uma variável, e depois a outra.
Passo 2
Para desenhar o mapa de contorno:
(Para
Quando , .
Essa é a equação da elipse com eixos:
e
Variando , chega-se ao seguinte mapa de contorno:
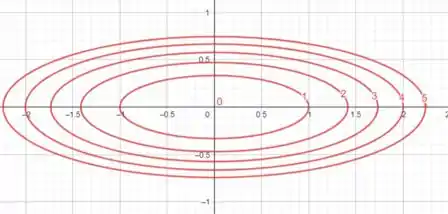
Veja que para cada , se fizermos por exemplo:
E para :
Conseguiremos encontrar os pontos de intersecção da curva com o eixo.
Passo 3
Para desenhar o gráfico da função:
Veja que para diferentes valores de temos a figura um paraboloide elíptico como mostrado na figura:
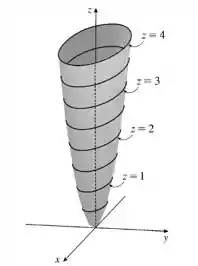
É interessante perceber que o mapa de contorno é a projeção da função no plano .
O solido em é uma extensão da planificação que encontramos em sua curva de nível, unindo todas as curvas, temos um solido.
Resposta
