Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 15
Encontre e esboce o domínio da função.
Passo 1
Queremos determinar o domínio de . Ou seja, queremos saber quais valores de , que podem ser usados para que seja real.
Para definir o domínio, vamos olhar para asretrições.
Temos que
Sabemos que
Ou
Ou ainda
Passo 2
Logo, o domínio é:
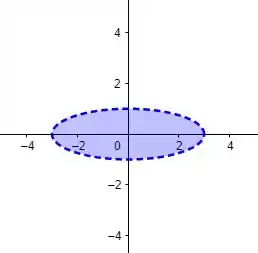
Pode-se perceber que se trata do interior de uma elipse, como mostrado na figura abaixo:
Resposta
Exercícios de Livros Relacionados
Raciocinando geometricamente, determine, caso existam, os valores máximo e mínimo de f em A, bem como os pontos em que estes valores são atingidos. f x , y = x + yeA = x , y ∈ I R 2x ≥ 0 , y ≥ 0, x +
Determine, caso existam, os valores máximo e mínimo de f em A; determine, também os ponrots em que esses valores são atingidos f x , y = x yeA = x , y ∈ I R 2 4 x 2 + y 2 = 1 ,y ≥ 0 }
Determine, caso existam, os valores máximo e mínimo de f em A; determine, também os ponrots em que esses valores são atingidos f x , y = x yeA = { ( x , y ) ∈ I R 2 | x ≥ 0ey ≥ 0 }
Determine, caso existam, os valores máximo e mínimo de f em A; determine, também os ponrots em que esses valores são atingidos f x , y = x ² x 2 + y ²eA = { ( x , y ) ∈ I R 2 | ( x , y ) ≠ ( 0,0 ) } ²
Determine, caso existam, os valores máximo e mínimo de f em A; determine, também os ponrots em que esses valores são atingidos f x , y = x - 1 2 + y - 1 ² + 3eA = I R ² ² ²