Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.3 - Ex. 42
Esboce a curva com a equação dada.
Passo 1
Olá galera. Pronto para mais uma questão? Segue a dica para resolvermos.
Primeiro podemos identificar qual curva a equação representa, a partir disso aplicar valores para para encontrarmos e constuirmos o gráfico.
Vamos começar!!!
Passo 2
O que a equação representa?
Nas equações polares o representa a distância do ponto até a origem e o o ângulo do ponto em relação ao eixo horizontal positivo.
Nessa equação não temos um termo constante, e não vai ser tão simples mudar para coordenadas cartesianas, e mesmo assim não seria uma equação que reconheceríamos como algo conhecido, então vamos na raça.
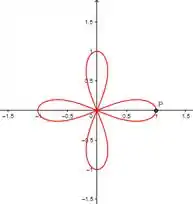
Mas ainda sim podemos idenficar a curva através da relação trigonométrica , essa curva é conhecida como uma rosácea de quatro pétalas.
Passo 3
Primeiramente vamos manipular a equação para isolar o sem expoente
Aplicando a raiz quadrada em ambos os lados temos:
Agora calculando os valores da função para igual à e
Passo 4
Analisando entre esses valores, em cada quadrante o argumento do cosseno vai dar uma volta inteira, então em todos os quadrantes o comportamento será o mesmo.
- No primeiro quadrante (), a curva começa próxima ao eixo positivo e se afasta gradualmente à medida que aumenta. O valor de é determinado pela variação de nesse intervalo.
- No segundo quadrante (), a curva continua a se afastar do eixo positivo, com influenciando a distância radial . A forma da curva reflete a mudança na função trigonométrica nesse intervalo.
- No terceiro quadrante (), a curva se aproxima do eixo negativo à medida que continua a aumentar. O sinal negativo de faz com que diminua, moldando a forma da curva nesse trecho.
- No quarto quadrante (), a curva continua sua trajetória em direção ao eixo negativo, com continuando a variar e influenciar . A forma da curva se completa ao redor da origem, formando a rosácea de quatro pétalas.
Passo 5
Desta forma nosso gráfico vai ter essa cara:
Resposta
