Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.3 - Ex. 40
Esboce a curva com a equação dada.
Passo 1
Oiii, tudo bem? Bom... o enunciado nos deu a seguinte equação polar:
Nas equações polares o representa a distância do ponto até a origem e o o ângulo do ponto em relação ao eixo horizontal positivo.
Queremos esboçar esse gráfico.
Então como faremos isso???
Bom... Nessa equação não temos um termo constante, e não vai ser tão simples mudar para coordenadas cartesianas, e mesmo assim não seria uma equação que reconheceríamos como algo conhecido...
Então vamos colocar alguns valores para e substituir na equação a fim de analisarmos o seu comportamento!! 😉
Passo 2
Primeiramente calculamos valores de para alguns valores de :
Vamos calcular para :
Para :
Para :
Para :
Para :
Passo 3
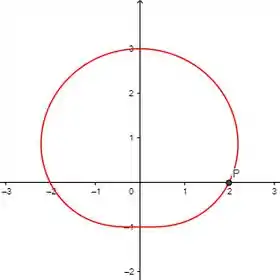
Como não tem variações bruscas entre esses valores e nem valores negativos vamos para o plano:
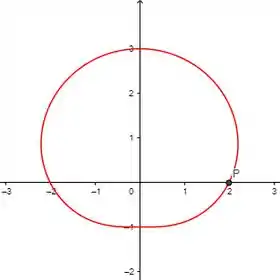
Em termos mais simples, a curva resultante dessa função polar mostra como a distância de um ponto à origem varia à medida que giramos ao redor dela (em torno do eixo , por exemplo).
A forma específica da curva é influenciada pelo comportamento do seno, resultando em uma curva que oscila de forma regular e se afasta da origem, devido ao termo constante adicionado.
Resposta
