Seja h x = x ,s ex0 x 2 ,s e0x ≤ 2 8 - x ,s ex2 Calcule, se existirem, os limites. i lim x → 0 + ⁡ h ( x ) , i i lim x → 0 ⁡ h x ,i i i lim x → 1 ⁡ h ( x ) i v lim x → 2 - ⁡ h ( x ) ,v lim x → 2 + ⁡ h ( x ) , v ilim x → 2 ⁡ h ( x ) Esboce o gráfico de h .

( a ) i lim x → 0 + ⁡ h ( x ) = lim x → 0 + ⁡ x 2 = 0 i i lim x → 0 ⁡ h x = 0 i i i lim x → 1 ⁡ h ( x ) = lim x → 1 ⁡ x 2 = 1 i v lim x → 2 - ⁡ h ( x ) =l i m x → 2 -x 2 = 4 v lim x → 2 + ⁡ h ( x ) = l i m x → 2 +8 - x = 6 v ilim x → 2 ⁡ h ( x ) ,n ã oe x i s t ep o i so sl i m i t e sl a t e r a i ss ã od i f e r e n t e s . ã ã ( b )

Enunciado

Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.3 - Ex. 48

Seja

Calcule, se existirem, os limites.

Esboce o gráfico de .

Passo 1

Opa, bora lá! Temos a função:

E temos que calcular alguns limites! Para isso devemos observar o intervalo e lembrar que o sinal de em cima do número indica pela direita e o sinal de pela esquerda do valor em análise. Assim:

Passo 2

Plotando nosso gráfico, ficaremos com:

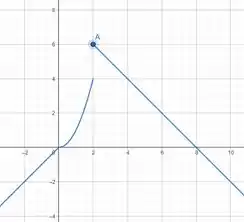
Prontinho!

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule, caso exista. Se não existir, justifique.underset(x - 1 ⁺)(lim) (|x - 1|)/(x - 1) ⁺

Calcule, caso exista. Se não existir, justifique.underset(x - 2 ⁻)(lim) (x^2 - 2 x + 1)/(x - 1) ⁻

Dada a função f x = x 2 - 3 x + 2 x - 1 , verifique que lim x → 1 ⁺ ⁡ f x = lim x → 1 ⁻ ⁡ f x ⁺ ⁻ . Pergunta-se: f é contínua em 1 ? Por quê?

Calcule, caso exista. Se não existir, justifique.underset(x - 1)(lim) (|x - 1|)/(x - 1)

Sejam f uma função definida num intervalo aberto I e p ∈ I . Suponha que f x ≤ f p para todo x ∈ I . Prove que lim x → p ⁡ f x - f p x - p = 0 desde que o limite exista.Sugestão: estude os sinais de l