Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.3 - Ex. 40
Encontre, quando existir, o limite. Caso não exista, explique por quê.
Passo 1
Fala aí! tudo certinho?
Nesse problema temos que verificar se o limite
Existe ou se não existir temos que explicar o motivo que nos levou ao resultado...
Parece complicado?
Nesse caso estamos trabalhando com uma função modular e está tendendo a , ou seja, tende a valores próximos a só que pela esquerda.
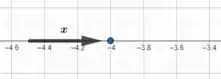
Dessa forma a maneira mais simples de resolver esse problema é fazer uma analise de sinais no numerador do limite para eliminar esse módulo.
Veja só!
Passo 2
No numerador do limite temos
E nosso tende a pela esquerda...
Isso quer dizer que está se aproximando de para valores infinitesimalmente menores que , ou seja, , ....
Perceba que se o conteúdo dentro do modulo será negativo. Então uma maneira de nos livrarmos do modulo é fazer
(OBS: Só funciona para )!!!
Substituindo essa simplificação no limite, chegamos em
Podemos simplificar da fração cortando em cima e em baixo
Como o limite de uma constante é a própria constante, temos
E aí! o que achou? Responde Aí!