Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 1.1 - Ex. 46
Encontre uma expressão para a função cujo gráfico é a curva dada.
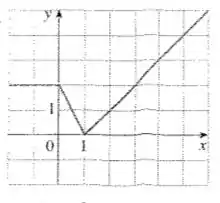
Passo 1
Fala aí, pessoal!
Aqui a gente tem um gráfico de uma função e precisa achar a expressão pra essa função.
Primeiramente devemos observar que o intervalo de análise para nós em vai ser o seguinte:
que é onde a função tá definida!
Além disso, devemos reparar que nossa função vai ser definida por intervalos, então na verdade é como se a gente tivesse que achar 3 funções, só que cada uma vai valer pra diferentes intervalos.
Já começando as análises, um dos intervalos () é constante e igual a . Nos outros dois intervalos, temos retas com diferentes inclinações. Então antes de qualquer coisa, vamos lembras da equação da reta:
onde é o coeficiente linear e é o coeficiente angular, dado por:
Então vamos calcular essas retas na prática!
Passo 2
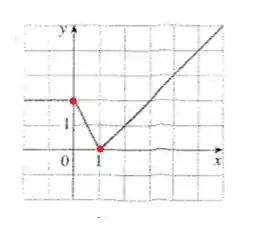
No intervalo , temos os seguintes dois pontos pertencentes a essa reta:
Então o coeficiente angular vai ser:
E o coeficiente linear é o ponto em que a reta cruza o eixo , então:
E essa reta fica:
Passo 3
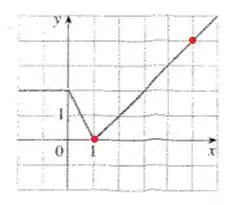
No intervalo , temos os seguintes dois pontos pertencentes a essa reta:
Então o coeficiente angular vai ser:
Aqui não conseguimos achar o coeficiente linear apenas olhando no gráfico. Então vamos pegar a equação geral da reta e substituir o que calculamos:
E agora substituir um ponto qualquer dessa reta. Eu escolhi o ponto :
E essa reta fica:
Passo 4
Por fim, o trecho inicial da nossa função, no intervalo , temos uma reta constante de valor 2, então neste trecho, a expressão é:
Juntando essas 3 informações, temos a expressão final da função: