Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 1.1 - Ex. 45
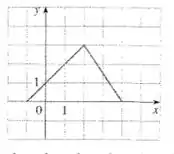
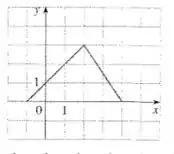
Encontre uma expressão para a função cujo gráfico é a curva dada.
Passo 1
Fala aí! tudo certinho?
Desejamos achar uma expressão para a função que é descrita através do gráfico dado.
Parece complicado?
Primeiramente devemos observar que o intervalo de análise para nós em vai ser o seguinte: . Além disso, devemos reparar que nossa função vai ser definida por intervalos onde um intervalo contém os pontos , e o outro intervalo contém os pontos .
Então vamos definir uma função que define a região e outra função que define a região .
Veja só!
Passo 2
Perceba que o gráfico do enunciado é composto por duas retas... uma no primeiro intervalo em e outra no segundo intervalo .
A equação da reta é dada pela função
E é o coeficiente angular dado por
Para resolver esse problema temos que determinar dois pontos em cada uma das retas...
Analisemos primeiramente o intervalo
Logo, tomando o ponto como referência, nossa reta será
Tranquilo até aqui?
Passo 3
Já para o intervalo teremos
Tomando o ponto como referência vamos ter
Juntando ambos os resultados em cada um dos seus intervalos, vamos obter
E aí! entendeu tudo? Responde Aí!