Encontre uma fórmula para a área do triângulo delimitado pela reta tangente ao gráfico de em , a reta horizontal por e o eixo

Nós temos uma função , antes de encontrar a área do triângulo, precisamos encontrar a equação da reta no ponto , e para isso, devemos calcular a derivada da função :

Aplicando na equação da reta no ponto , temos que :

O triangulo pode ser delimitado pelo ponto que passa pela linha tangente, como podemos ver no gráfico:

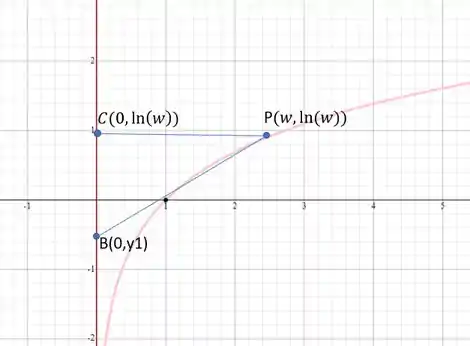
Com a equação tangencial encontrada, podemos calcular o ponto

Se :

A coordenada

Como sabemos que o triangulo é delimitado pelos pontos e , ainda existe o ponto que também passa pela origem no , e tem sua coordenada no na mesma posição que o ponto , pois a o triângulo é delimitado pela reta tangente e os eixos da coordenada. O que nos da, o seguinte conjunto de pontos:

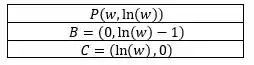
Mas, lembre-se: precisamos calcular a área do triângulo.