Use um gráfico para decidir se é um a um.
Passo 1
Olá, meu querido estudante. Pronto para mais uma resolução?
Aqui a gente tem uma atividade que nos pede para dizermos, por meio do gráfico, se a função dada é um a um.
Primeiro vamos falar da função um a um:
A função um a um (ou função bijetiva) é uma função em que cada elemento do domínio está relacionado a um único elemento do contradomínio e cada elemento do contradomínio está relacionado a um único elemento do domínio. Em outras palavras, não há repetição nos elementos associados.
Para identificar graficamente se uma função é uma função um a um, você pode usar o teste da linha horizontal:
1. Desenhe o gráfico da função.
2. Trace uma linha horizontal em todo o gráfico.
3. Veja se a linha horizontal cruza o gráfico em mais de um ponto em qualquer lugar.
Se a linha horizontal cruzar o gráfico em mais de um ponto em qualquer lugar, então a função não é uma função um a um, pois isso significaria que dois valores diferentes do domínio estão sendo mapeados para o mesmo valor no contradomínio.
Se a linha horizontal cruzar o gráfico em apenas um ponto em todos os lugares, então a função é uma função um a um, pois isso significaria que cada valor no domínio é mapeado para um único valor no contradomínio.
Passo 2
O gráfico da função
Está plotado logo abaixo:
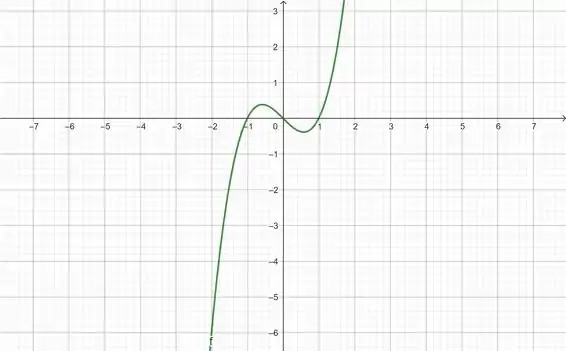
Neste caso, não precisamos nem traçar nenhuma linha horizontal, pois a própria linha do eixo mostra que temos 3 raízes, então nossa função não é um a um, pois temos 3 valores diferentes mas que possuem imagens iguais.
Resposta
Não é um a um