Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 1.1 - Ex. 43
Encontre para as funções dadas. Então esboce os gráficos das funções.
Passo 1
Eaee, belezinha?? Bom... o enunciado nos deu a seguinte função:
Queremos encontrar e.
Para isso, basta analisarmos o intervalo em que o valor de se encaixa de acordo com a condição da função.
Em seguida, devemos esboçar o gráfico dessa função.
Para isso, basta analisarmos que para precisaremos de dois pontos para traçar uma reta (já que para essa condição a função é uma reta).
Por outro lado, para , basta analisarmos que a condição da função descreve uma parábola com concavidade voltada para cima com vértice no zero.
Bora lá!! 😉
Passo 2
Então, para temos que nesse caso, , portanto:
Para temos que , logo:
Por fim, para temos que , logo:
Passo 3
Para traçar o gráfico, temos que fazer em partes.
Para a equação da reta quando , já temos o ponto .
Agora vamos fazer para pegarmos outro ponto:
Logo, o nosso par de pontos para a condição é:
Para , já temos dois pontos do enunciado e sabemos que é uma parábola por ser uma equação do segundo grau.
Passo 4
Com essas informações, podemos plotar o gráfico:
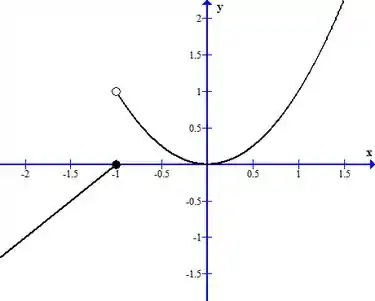
Resposta
