Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 1.1 - Ex. 41
Encontre para a função definida por partes. A seguir, esboce o gráfico da função.
Passo 1
Eaee, belezinha?? Bom... a questão nos dá a seguinte função definida por partes:
Queremos encontrar os valores pedidos para a função acima. Para isso, basta substituirmos o valor entre parênteses no lugar de . Mas como? Substituímos em ou em ?
Isso vai depender do valor de , temos que avaliar se o número é maior, menor ou igual a zero antes. Se for maior ou igual 0, usamos . Se é menor que 0, usamos .
Por fim, vamos esboçar o gráfico da figura com base nos intervalos dados na função.
Então bora junto!!
Passo 2
Então.. como é menor que zero, então pegamos a primeira parte da função:
Como é igual a zero, então pegamos a segunda parte da função:
Por fim, como é maior que zero, então pegamos a segunda parte da função:
Passo 3
Para traçar o gráfico, temos que fazer em partes. Como são retas, bastam pontos para definir o esboço.
Primeiro vamos fazer para . Nesse intervalo, trabalhamos com , então:
em , temos
em temos
Para , trabalhamos com , então:
em , temos
em , temos
No gráfico:
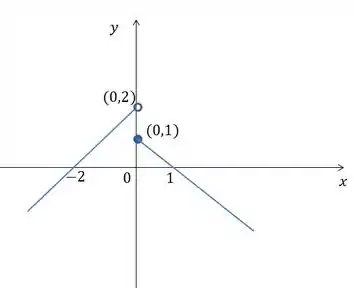
Entendeu direitinho?? Responde aee 😉
Resposta
