Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 4.1 - Ex. 7
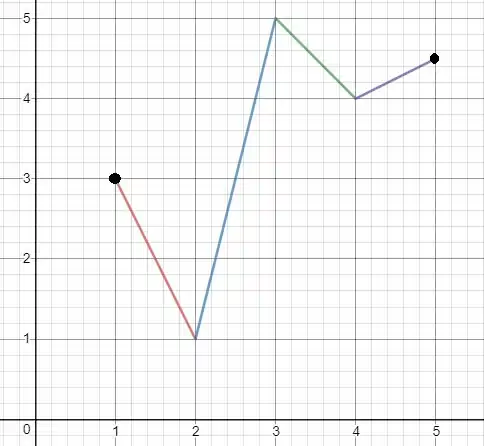
Esboce o gráfico de uma função que seja contínua em e tenha as propriedades dadas:
Máximo absoluto em , mínimo absoluto em e mínimo local em .
Passo 1
Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
Devemos esboçar o gráfico de uma função contínua (sem buracos ou saltos) no intervalo
seja o mínimo global
seja o máximo global
seja o mínimo local
Então essa função vai de 1 a 5 e tem esse comportamento acima.
Que função será que apresenta esse comportamento?
Passo 2
Escolhemos o valor para de modo que, no gráfico que esboçamos, o máximo absoluto seja o ponto mais alto, enquanto o ponto mais baixo no gráfico seja o mínimo absoluto.
Os valores podiam ser muitos, essa é apenas uma das funções que atende esses requisitos. O que importa é o máximo global ser o mais alto, o mínimo global o mais baixo e o mínimo local estar entre eles.
Um gráfico que satisfaz todas as propriedades é:
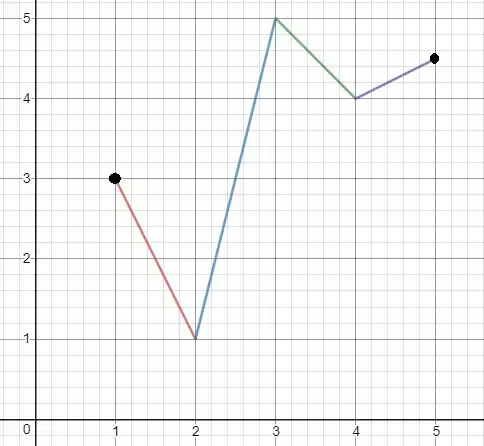
Poxa mas eu pensei que a função precisava ser definida por uma única lei
Não necessariamente! Ela precisa ser uma função e contínua (sem buracos ou saltos).
Resposta
