Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.7 - Ex. 4
- Encontre a inclinação da reta tangente à parábola no ponto
- Usando a definição 1
- Usando a equação 2
- Encontre a equação da reta tangente da parte (a)
- Faça os gráficos da parábola e da reta tangente. Como verificação, dê um zoom em direção ao ponto até que a parábola e a reta fiquem indistinguíveis.
- Usando a definição 1
- Usando a equação 2
Passo 1
Fala aí! tudo certinho? 😉
Nesse problema temos que obter a inclinação da reta tangente à no ponto . Pra isso vamos usar as duas definições.
Além disso vamos obter a equação da reta tangente a esse ponto e obter o gráfico da função e da reta tangente.
Parece complicado? 😊
A primeira definição para obter a inclinação da reta é dada por
Já a segunda definição é dada por
A partir de , podemos definir a equação da reta tangente como
Onde e são as coordenadas do ponto
Saca só! 😐
Passo 2
Usando a definição 1, temos
Se , então
Substituindo e ...
Podemos simplificar o numerador, colocando em evidência
Perceba que temos como fatorar
Assim conseguimos simplificar no numerador e no denominador
Calculando o limite...
Tranquilo até aqui? 😁
Passo 3
Usando a equação 2
Substituindo e para , temos
Simplificado...
Perceba que podemos colocar em evidencia no numerador e simplificar com o denominador
Aplicando o limite
Legal, né? 😉
Passo 4
A equação da reta tangente pode ser calculada por
Se , e ...
Bacana? 😬
Passo 5
Para esboçar o gráfico, a questão nos disse para usar uma calculadora gráfica...
Portanto, plotando os gráficos da função e da reta tangente, temos
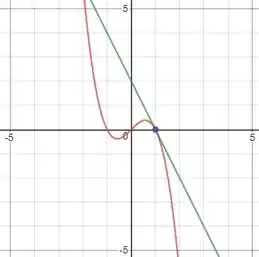
E dando um zoom no ponto
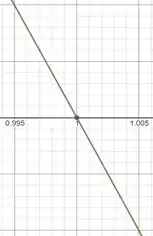
E aí! entendeu tudo? Responde Aí! 😉