Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.7 - Ex. 10

a) Encontre a inclinação da tangente à curva y = 1 / x no ponto onde x = a

b) Encontre as equações das retas tangentes nos pontos 1,1   e   4   , 1 2    

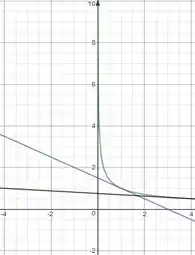
c) Faça o gráfico das curvas e de ambas as retas tangentes em uma mesma tela

Passo 1

Fala aí, pessoal! 😉

Nesse problema queremos obter a inclinação de y = 1 x em x = a , as retas tangentes em 1,1 e 4 , 1 2 e esboçar o grafico de todas essas curvas.

Muita coisa, né? 👀

Para o item a) podemos obter a inclinação de f em a pelo método da tangente pelo limite

m = lim x → a ⁡ f x - f a x - a

Com a inclinação de f para qualquer ponto em mãos, podemos obter as retas tangentes substituindo x = a e aplicando na formulinha

y - y 1 = m x - x 1

Veja só! 😬

Passo 2

Calcularemos pela definição 1 o valor da inclinação da tangente. Então

m = lim x → a ⁡ f x - f a x - a = lim x → a ⁡ 1 x - 1 a x - a

m = lim x → a ⁡ a - x x ⋅ a ⋅ x - a

Multiplicando o numertador e o denominador de f pelo conjugado do numerador, temos

m = lim x → a ⁡ a - x x ⋅ a ⋅ x - a ⋅ a + x a + x

m = lim x → a ⁡ a - x x ⋅ a ⋅ x - a ⋅ a + x

m = lim x → a ⁡ a - x - x ⋅ a ⋅ a - x ⋅ a + x

m = lim x → a ⁡ - 1 x ⋅ a ⋅ a + x

m = - 1 a 2 ⋅ a + a = - 1 a ⋅ 2 ⋅ a

E finalmente...

m = - 1 2 a 3

Legal, né? 😉

Passo 3

Agora encontraremos a equação da reta tangente no ponto ( 1,1 ) , basta substituir a = 1 na inclinação da tangente encontrada no item (a)

m = - 1 2 1 3

m = - 1 2

Daí, a equação da reta tangente será

y - y 1 = m x - x 1

y - 1 = - 1 2 x - 1

y = - 1 2 x + 1 2 + 1

y = - x + 3 2

Tranquilo até aqui? 😎

Passo 4

Agora encontraremos a equação da reta tangente no ponto ( 4   , 1 2 ) , basta substituir a = 4 na inclinação da tangente encontrada no item (a)

m = - 1 2 4 3

m = - 1 16

Daí, a equação da reta tangente será

y - y 1 = m x - x 1

y - 1 2 = - 1 16 ( x - 4 )

y = - x 16 + 1 4 + 1 2 = - x 16 + 1 4 + 2 4

y = - x 16 + 3 4 = - x + 12 16

y = - x + 12 16

Estamos quase lá! 😉

Passo 5

Esboçando os gráficos

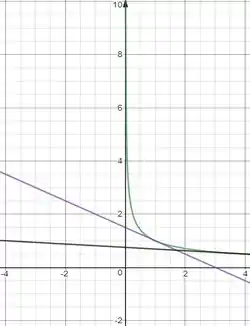
E aí! o que achou? Responde Aí! 😁

Resposta

a) m = - 1 2 a 3

b) y = - x + 3 2 ,     y = - x + 12 16

c)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache uma equação de reta tangente ao gráfico da função seno no ponto x = 0 x = π 3 x = π
Prove que a reta tangente à curva y = - x 4 + 2 x 2 + x no ponto ( 1 ,2 ) é também tangente à curva em um outro ponto e determine esse ponto
Ache as equações das retas tangente e normal à curva y = 8 s e n 3 2 x no ponto π 12 ,1 .
Ache uma equação da reta normal à curva x - y = sqrt(x + y) no ponto ( 3 , 1 )
Ache as equações das retas tangentes à curva y = 2 x 3 + 4 x 2 - x que têm inclinação 1 2 .