Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 5.5 - Ex. 20
Encontre a integral indefinida geral.
Passo 1
Opa, bora calcular essa integral aqui:
Pra isso vamos utilizar o método de substituição simples! Uma dica legal pra escolher quem vai ser o é pensar:
“o que, que, se eu substituir por vai transformar essa integral em uma integral mais simples de resolver?!”
O geralmente vai ser a parte mais complicadinha da nossa função e depois derivamos ele pra achar e fazer a substituição!
A ideia é que du seja igual tudo que restou, pra que toda nossa integral fique em função de u. Nem sempre dá pra fazer isso de uma forma direta, as vezes vamos precisar de uns truquezinhos. Vem comigo que eu te mostro!
Feito isso bora integrar, e para isso vamos usar nossa tabela de primitivas:
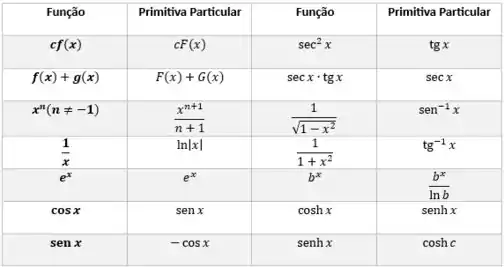
E por fim, mas não menos importante, vamos voltar o valor de para o valor original!
Ufa! Agora mão na massa!
Passo 2
Nosso será a função mais complicada, neste caso ao cubo é mais complicado que ao quadrado, assim:
Agora calculamos :
Agora vamos substituir em nossa integral:
Agora ficamos com uma integral bem simplinha de resolver!
Chegamos em uma integral que está na nossa tabela:
E não esquece da constante em?
Então temos:
Lembrando que , então vamos substituir:
Prontinho! Resolvemos!
Responde Aí!
