Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.3 - Ex. 12
Se , encontre e e interprete esses números como inclinações. Ilustre com esboços desenhados à mão ou gráficos de computador.
Passo 1
Opa, tudo tranquilo? Questãozinha de derivadas parciais, vamos lá!
A questão nos dá uma função e nos pede suas derivadas parciais no ponto . Pra fazer isso a gente lembra que pra determinar derivadas parciais, é necessário fixar as variáveis que não estão envolvidas na derivação e tratá-las como valores constantes.
Depois de fazer isso, temos ainda que esboçar essas derivadas parciais como inclinações, isto é, a questão quer que a gente associe o conceito de derivadas (que era reta tangente, lembra?) no desenho do gráfico original!
Passo 2
Antes de qualquer coisa temos que encontrar as derivadas parciais, né?
Seja a função
Para determinar fixamos o valor de e derivamos em relação a . Assim, temos:
Derivando utilizando a regra da cadeia temos:
Da mesma forma, para determinar fixamos o valor de e derivamos em relação a . Assim, temos:
Derivando utilizando a regra da cadeia temos:
Passo 3
Agora basta substituir os valores de e , respectivamente, nas derivadas parciais encontradas.
Passo 4
Para modelar o gráfico temos algumas opções:
O MATLAB é a melhor opção, perfeito pra qualquer questão assim, mas além de pago ele é um software bem pesado. Aí que entra o GeoGebra: Além de ser gratuito ele ainda roda no navegador!
O processo vai ser o seguinte: Pesquise por “GeoGebra” no navegador (ou vá nesse link: geogebra.org/calculator), selecione “Calculadora 3D” e insira a função e o ponto no campo “Entrada”.
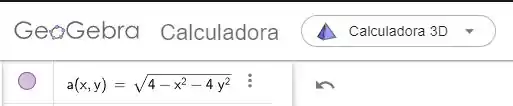
Você vai ver algo assim:
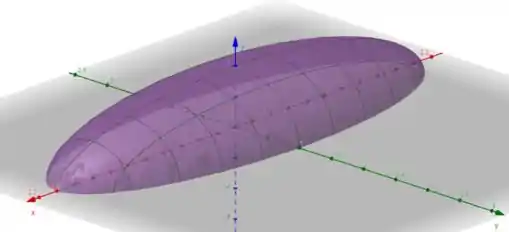
Mas queremos demonstrar os valores das derivadas que encontramos como retas tangentes a esse gráfico. Para isso, usando o valor da inclinação que encontramos e o ponto no gráfico que já temos, podemos desenhar as retas!
Obs.: Para desenhar as retas você pode usar a função Segmento em dois pontos que pertençam à reta tangente.
Quando a derivada parcial é em relação a :
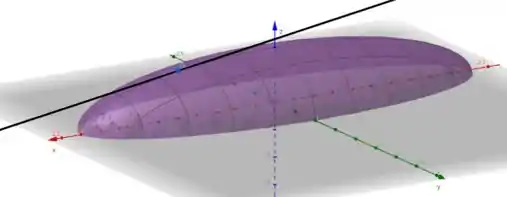
Quando a derivada parcial é em relação a :
O objetivo desse item era nos fazer associar o conceito de derivadas que tínhamos com o novo conceito de derivadas parciais. Observe, por exemplo, na reta que demonstra , o valor de é constante e conforme cresce, o valor da função diminui.