Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.3 - Ex. 6

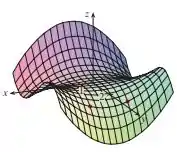
Determine os sinais das derivadas parciais da função f cujo gráfico é mostrado

6 .     a )   f x ( - 1,2 )

b) f y ( - 1,2 )

Passo 1

Fala, galera! Beleza?

Nessa questão nós temos o gráfico de uma função f e queremos saber o sinal da derivada em um certo ponto. Em particular, nos itens a) e b), nós temos que determinar o sinal da derivada parcial de f com relação a x   e y   no ponto - 1,2 .  

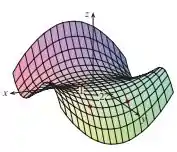
Para isso, no item a), vamos fixar y e olhar o ponto e pedido, analisando somente a variação da função no plano X Z .

Depois, no item b), vamos fixar x e olhar o ponto e pedido, analisando somente a variação da função no plano Y Z .

Vem comigo que eu te explico!

Passo 2

a)Para determinar o sinal de f x - 1,2 , fixamos y = 2 e verificamos a variação de x , seguindo no sentido positivo do eixo   x e partindo de x   = -   1 . Observa-se que a função decresce, isto é, f x - 1,2 é negativo.

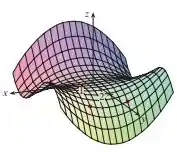
Passo 3

b)Para determinar o sinal de f y - 1,2 , fixamos x = - 1 e verificamos a variação de y , seguindo no sentido positivo do eixo y e partindo de y   =   2 . Observa-se que a função decresce, isto é, f y - 1,2 é negativo.

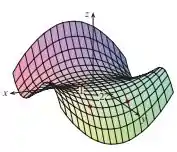
Resposta

  1. Negativo
  2. Negativo
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dizemos que ( x 0 , y 0 ) é um ponto crítico do estacionário de z = f ( x , y ) se ∂ f ∂ x x 0 , y 0 = ∂ f ∂ y x 0 , y 0 = 0 . Determine (caso existam) os pontos críticos da função f x , y = 3 x 2 + 8
Seja f x , y = x 2 + y 2 e seja γ t = t , t , z t , t ∈ R , uma curva cuja imagem está contida no gráfico de f .a) Determine z t .b) Esboce os gráficos de f e γ .c) Determine a reta tangente a γ no po
Seja f x , y = 2 x y 2 x 2 + y 4 s ex , y ≠ 0,0 0 s ex , y = 0,0 e seja γ t = t , t , z ( t ) , t ∈ R uma curva cuja imagem está contida no gráfico de f . Seja T a reta tangente a γ em γ 0 . Mostre qu
Suponha que z = f x , y admita derivadas parciais em ( x 0 , y 0 ) . Considere as curvas cujas imagens estão contidas no gráfico da f : γ 1 = x = x 0 y = t z = f ( x 0 , t ) e γ 2 = x = t y = y 0 z =
Considere a função z = f x , y . Como você definiria o plano tangente ao gráfico de f no ponto ( x 0 , y 0 ) ? Admitindo que f admita derivadas parciais em x 0 , y 0 , escreva a equação do plano que v