Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.3 - Ex. 10
O seguinte mapa de contorno é dado para uma função . Use-o para aproximar e .
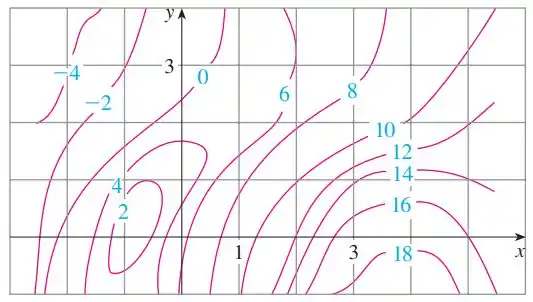
Passo 1
Opa, tudo tranquilo? Questãozinha de derivadas parciais, vamos lá! A questão nos dá um mapa de contorno de uma função e pede para encontrarmos e no ponto , mas como fazer isso?
Primeiro precisamos interpretar esse gráfico! Podemos visualizar esse mapa de contorno como a visão superior de um gráfico 3D, as curvas de nível (as linhas rosa) mostram o contorno da função (ou o eixo , para simplificar) em uma altura qualquer (os números azuis).
Além disso, sabemos que e são derivadas parciais de ! Se tivéssemos a função nós calcularíamos essas derivadas de forma simples: Para , por exemplo, nós trataríamos como um valor constante e derivaríamos em !
Mas vocês lembram que a derivada é a inclinação da reta tangente? Nós podemos calcular as derivadas parciais da mesma forma aqui!
Para nós fixamos (o valor da questão) e calculamos a inclinação usando os valores das curvas de nível e os respectivos valores de !
Passo 2
Para estimar o valor de em nós fixamos o valor de
E observe que para o valor das curvas de nível está aumentando: A primeira curva tem valor em e a próxima em !
Daí só precisamos calcular a inclinação (ou a taxa de variação, como preferir)!
Passo 3
Da mesma forma, para estimar o valor de fixamos
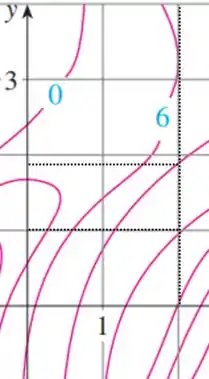
E observamos que conforme aumenta, o valor da função diminui: A primeira curva tem valor em e a próxima em !