Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.3 - Ex. 17

(a) Encontre os intervalos nos quais f é crescente ou decrescente.

(b) Encontre os valores máximo e mínimo locais de f.

(c) Encontre os intervalos de concavidade e os pontos de inflexão.

f x = x 2 - x - ln ⁡ x

Passo 1

Fala, galera! Beleza? Vamos resolver essa questão!

O enunciado pediu pra gente encontrar os intervalos de crescimento e decrescimento da função, seus valores de máximo e mínimo locais e também seus intervalos de concavidade e pontos de inflexão.

Bastante coisa, né? Mas tudo isso pode ser resolvido com a ajuda da nossa amiga derivada. Pra isso, vamos derivar a nossa função e igualar o resultado a zero, para obter os pontos críticos. Em seguida, vamos avaliar o sinal dessa derivada, usando os pontos críticos encontrados. Esses intervalos vão determinar onde a função é crescente ou decrescente.

Depois, vamos usar o Teste da segunda derivada, para determinar os valores de máximo e mínimo locais de f . E por fim, vamos analisar o sinal dessa segunda derivada (o que vai nos indicar os intervalos de concavidade) e igualar ela a zero, para encontrar os pontos de inflexão.

Vamos lá!

Passo 2

Para achar os números críticos de f , derivamos:

f ' x = 2 x - 1 - 1 x

Tirando o M.M.C:

f ' x = 2 x 2 - x - 1 x

Fatorando:

f ' x = ( 2 x + 1 ) ( x - 1 ) x

Igualando esse resultado a zero:

2 x + 1 x - 1 = 0

Pra que esse produto seja verdadeiro, um dos termos precisa ser zero. Então, temos:

2 x + 1 = 0 → x = - 1 2

x - 1 = 0 → x = 1

Passo 3

Testando f ' ( x ) nos intervalos determinados pelos pontos críticos, temos:

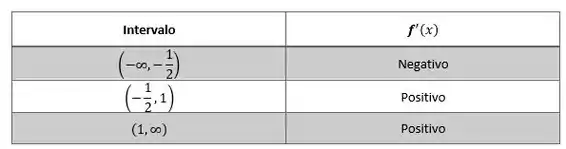
Então, a função será crescente em:

- ∞ ,   - 1 2 ∪ - 1 2 ,   1

E será decrescente no intervalo:

( 1 ,   ∞ )

Passo 4

Agora para verificar os valores de máximo e mínimo, vamos usar o teste da segunda derivada. Pra isso, derivamos f ' ( x ) novamente e obtemos:

f ' ' x = 2 + 1 x 2

Substituindo os valores dos pontos críticos que encontramos no passo 2 , temos:

f ' ' - 1 2 = 8

f ' ' 1 = 3

Portanto, temos f ' ' - 1 2 > 0 , indicando que x = - 1 2 é um ponto de mínimo local. E da mesma forma, para f ' ' 1 > 0 , onde temos outro ponto de mínimo local em x = 1 .

Passo 5

Os pontos de inflexão ocorrem f ' ' x = 0 ou é indefinido. Não temos tais pontos nesse caso, pois f ' ' ( x ) é sempre positivo.

Além disso, como f ' ' ( x ) é sempre positiva, a função é sempre côncava para cima.

Valeu, galera! Até a próxima! 😉

Resposta

(a)

C r e s c e n t e → - ∞ ,   - 1 2 ∪ - 1 2 ,   1

D e c r e s c e n t e → ( 1 ,   ∞ )

(b) Mínimos locais em x = 1 e x = - 1 2

(c) A concavidade será sempre para cima e não existe ponto de inflexão, nesse caso.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um terreno retangular deve ser cercado de duas formas. Dois lados opostos devem receber uma cerca reforçada que custa $ 3 o metro enquanto os dois lados restantes recebem uma cerca padrão de $ 2 o met
Um retângulo deve ser inscrito em um triângulo retângulo com lados de comprimento 6, 8 e 10 cm. Encontre as dimensões do retângulo com a a maior área, supondo que ele está posicionado conforme a Figur
Um campo retangular está limitado por uma cerca em três de seus lados e por um córrego reto no quarto lado. Encontre as dimensões do campo com área máxima que pode ser cercado com 1000 m de cerca.
Encontre o ponto P do primeiro quadrante que pertença à curva y = x - 2 tal que um retângulo com lados nos eixos coordenados e um vértice em P tenha o menor perímetro possível.
Uma área retangular com 288m 2 deve ser cercada. Em dois lados opostos, será usada uma cerca que custa $ 1 o metro, e nos lados restantes uma cerca que custa $ 2 o metro. Encontre as dimensões do retâ