Encontre o ponto do primeiro quadrante que pertença à curva tal que um retângulo com lados nos eixos coordenados e um vértice em tenha o menor perímetro possível.
Passo 1
Uma imagem pode nos ajudar a raciocinar melhor sobre qual é a nossa situação:
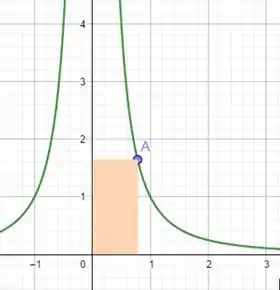
Esse é um típico exercício de otimização. O cálculo diferencial é uma ferramenta que nos ajuda muito na resolução desses casos, tão recorrentes no dia a dia.
Nesse caso, queremos inserir um retângulo com o menor perímetro possível sob essa curva, de forma que os lados do retângulo coincidam com os eixos e , e esteja no primeiro quadrante.
Passo 2
Temos que o perímetro é a soma dos lados do retângulo, que podemos chamar de , a base, e , a altura. Assim, escrevemos a equação pro perímetro :
Nisso, precisamos escrever o perímetro desse retângulo em função apenas de uma variável. No caso, vamos buscar escrever apenas em função de , pra termos uma .
Como correlacionamos e então? Bom, eles já estão correlacionados, pela própria equação da curva!
Temos que:
Assim, substituímos essa expressão de na equação do perímetro e vamos obter . Teremos:
Passo 3
Agora temos uma função que descreve nosso perímetro.
Queremos o ponto de mínimo, que vai nos dar o menor perímetro. E como fazer isso?
Se você ainda não sabe, ou talvez não lembre, mas um dos teoremas do Cálculo (Teorema de Fermat) diz que, nos pontos de máximo e de mínimo de uma função (quando possui) a derivada se anula.
Logo, podemos pegar , derivar e igualar a zero! Os valores de que acharmos atribuídos a essa derivada nula vão ser os pontos de máximo e mínimo.
Nisso, cabe a nós distinguir qual é qual, aplicando esses valores na função original e verificando qual nos dá o menor valor. Vai ser esse o nosso ponto de mínimo!
Passo 4
Derivando, temos:
Igualamos isso a zero:
Assim, esse é nosso ponto de derivada nula da função, que é o nosso ponto de mínimo. Assim, esse seria o tamanho da base do retângulo de menor perímetro que atende às condições pedidas. Então, equivale à coordenada do ponto !
Ainda precisamos de . Conseguimos obtê-lo pela equação da curva. Teremos:
Assim, essa é a coordenada do ponto , que é o ponto vértice do retângulo de menor perímetro cujos lados pertencem aos eixos coordenados, sob a curva .
Resposta
São as coordenadas e