Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.1 - Ex. 24
Encontre: (a) os intervalos nos quais é crescente, (b) os intervalos nos quais é decrescente, (c) os intervalos abertos nos quais é côncava para cima, (d) os intervalos abertos nos quais é côncava para baixo e (e) as coordenadas de todos os pontos de inflexão.
Passo 1
Para encontrar onde é crescente e decrescente temos que analisar a primeira derivada de , sabemos que é crescente quando é positiva, e é decrescente quando é negativa:
Vamos ver onde ela é igual a zero:
Temos que em é um ponto onde não há derivada, então temos que analisar o sinal em torno dele também.
Vamos então analisar o sinal agora:
- Temos então que é crescente em .
- E é decrescente em .
- Temos então que é côncava para cima em e .
- E é côncava para baixo em .
- Os pontos de inflexão ocorrem onde a concavidade muda, assim temos um ponto de inflexão em .
Passo 2
Já em relação a concavidade vamos analisar a segunda derivada, e aqui sabemos que é côncava para cima quando é positiva, e é côncava para baixo quando é negativa:
Vamos ver onde ela é igual a zero:
Temos que em é um ponto onde não há derivada, então temos que analisar o sinal em torno dele também.
Vamos analisar o sinal:
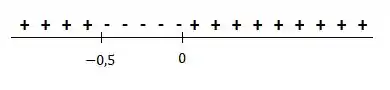
Passo 3
Resposta
- e