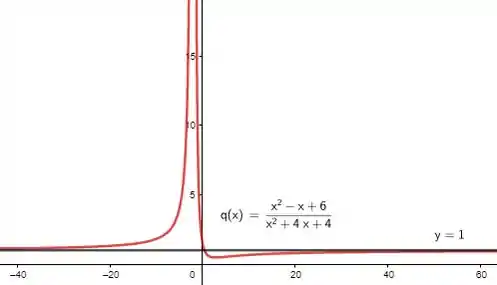
Nos exercícios de 49 a 56, encontre as assíntotas horizontal e vertical e faça um esboço do gráfico da equação
Passo 1
Vamos escrever isso como antes de mais nada, belezinha? Saca só:
Passo 2
Bora achar as assíntotas horizontais. Precisamos pra isso fazer os limites pros infinito, beleza?
Nos dois casos teremos
Limites deram números? Então beleza, temos uma assíntota horizontal!
Passo 3
Pras verticais, fazemos os limites pro ponto que “dá problema”. No caso, limites laterais pra , que é o único ponto que zera o denominador
Se os limites explodiram então temos duas assíntotas verticais!
Passo 4
Juntando os resultados dos limites, esboçamos:
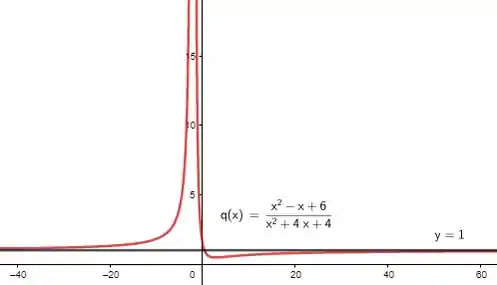
Resposta