Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.4 - Ex. 67
Use o roteiro para esboçar o gráfico da curva. No passo D, ache a equação para assíntota obliqua.
Passo 1
Oieee, tudo bem?
Bora resolver comigo?
Para esboçar o gráfico da curva, podemos seguir este roteiro:
1. Encontre os interceptos com os eixos x e y.
2. Determine os intervalos onde a função é positiva e negativa.
3. Encontre os pontos de inflexão, se houver.
4. Verifique a concavidade da curva.
5. Identifique assíntotas verticais e horizontais, se existirem.
6. Esboce a curva.
Vamos começar:
Intercepto y: Para encontrar o intercepto y, definimos na equação da função:
Como dividir por zero não é definido, não há intercepto y.
Passo 2
Intercepto Para encontrar o intercepto , definimos y = 0 na equação da função:
Isolamos x:
Portanto,
Assim, o intercepto x é
Passo 3
Intervalos de Positividade/Negatividade:
Observe que a função é positiva para e negativa para
Pontos de inflexão:
Para encontrar os pontos de inflexão, vamos calcular a segunda derivada da função e determinar onde ela muda de concavidade.
A função é
Vamos derivar duas vezes:
Passo 4
Vamos derivar mais uma vez:
Para encontrar os pontos de inflexão, resolvemos
Não há solução real.
Portanto, não há pontos de inflexão.
Passo 5
A concavidade da curva é determinada pelo sinal da segunda derivada.
Como para todo a curva é côncava para cima em todo o seu domínio.
- Assíntotas verticais: Elas ocorrem onde o denominador se torna zero, mas como o denominador é não há assíntotas verticais.
- Assíntotas horizontais: Podemos encontrar a assíntota horizontal encontrando o limite quando se aproxima do infinito:
Portanto, não há assíntotas horizontais.
Passo 6
Agora, vamos esboçar o gráfico da função com as informações que encontramos.
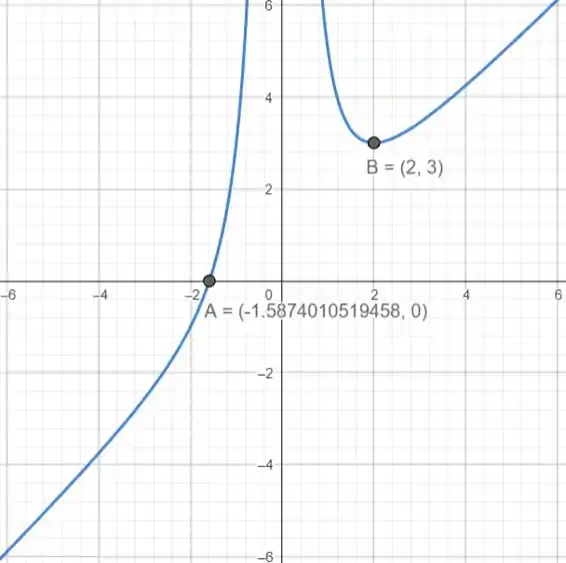
Resposta
Vide a explicação.