Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 4.4 - Ex. 19
Encontre o limite. Use a Regra de L’Hôspital quando for apropriado. Se existir um método mais elementar, use-o. Se a Regra de L’Hôspital não for aplicável, explique o por quê.
Passo 1
E aí, galerinha! 😁
Nesse problema temos apenas que calcular o limite.
A primeira coisa a se fazer aqui é verificar se temos uma indeterminação do tipo ou para aplicar a regra de L’Hôspital.
O e , temos algo como e não podemos aplicar L’Hôspital.
Passo 2
Vamos manipular a expressão para possamos utilizar a regra de L’Hôspital.
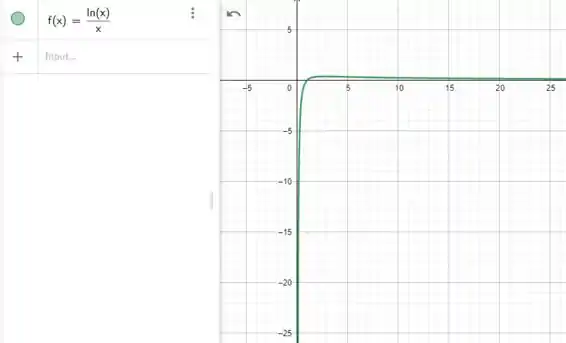
O gráfico abaixo irá nos ajudar a visualizar melhor o que encontramos matematicamente.
Resposta
Exercícios de Livros Relacionados
Encontre o limite. Use a Regra de L'Hôspital quando for apropriado. Se existir um método mais elementar, use-o. Se a Regra de L'Hôspital não for aplicável, explique por quê. lim x → ∞ ln x 2 x
Encontre o limite. Use a Regra de L'Hôspital quando for apropriado. Se existir um método mais elementar, use-o. Se a Regra de L'Hôspital não for aplicável, explique por quê. lim x → 1 x a - a x + a
Encontre o limite. Use a Regra de L'Hôspital quando for apropriado. Se existir um método mais elementar, use-o. Se a Regra de L'Hôspital não for aplicável, explique por quê. lim x → 0 x tg - 1 4 x
Encontre o limite. Use a Regra de L’Hôspital quando for apropriado. Se existir um método mais elementar, use-o. Se a Regra de L’Hôspital não for aplicável, explique o por quê. 34 . lim x → ∞ x 2 + 2
Encontre o limite. Use a Regra de L'Hôspital quando for apropriado. Se existir um método mais elementar, use-o. Se a Regra de L'Hôspital não for aplicável, explique por quê. lim x → 0 e x - 1 - x x