Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.4 - Ex. 38
Encontre o limite. Use a regra de L’Hôspital quando for apropriado. Se houver um método mais elementar, considere utilizá-lo. Se a regra de L’Hôspital não se aplicar, o porquê.
Passo 1
E aí, galerinha! 😁
Bom, essa questão pede pra gente usar a regra de L’Hospital para calcular o seguinte limite:
E se existir um método mais elementar, devemos usá-lo. Se a regra de L’Hospital não for aplicável, devemos explicar o porquê.
Então vamos relembrar que regra é essas para que a gente possa usar.
A Regra de L'Hôpital é um teorema que ajuda a gente a calcular limites de formas indeterminadas.
A regra diz que, nesses casos, o limite da fração é igual ao limite da derivada do numerador dividida pelo limite da derivada do denominador, supondo funções deriváveis no intervalo de interesse.
Assim, se
Ou se
Podemos fazer:
Agora vamos tentar calcular nosso limite.
Passo 2
Se calcularmos diretamente o limite podemos verificar se há a existência de uma indeterminação. E veja que:
Opa!
Temos um limite indeterminado, porém ele não é do tipo L’Hospital.
Para que fosse, nosso limite deveria ter caído em uma indeterminação na forma 0/0 ou /.
Sendo assim, vamos tentar fazer algumas modificações algébrica em nossa função pra ver se conseguimos um limite na forma correta para usar o L’Hospital.
Passo 3
Veja que o denominador se aproxima de , já que:
Para avaliar:
Vamos igualá-la a uma variável:
Então, colocando o logaritmo natural em ambos os lados:
Reescrevendo:
E isso nos dá uma indeterminação do tipo L’Hospital, uma vez que:
Passo 4
Lembrando que, como:
Podemos fazer:
Aplicando a regra em nossa função, devemos derivar as funções que estão no numerador e no denominador.
Assim,
Que pode ser escrita na forma:
E temos:
Assim, podemos dizer concluir que:
Então
Passo 5
Voltando agora ao limite original:
Uma forma de vermos isso é através do gráfico:
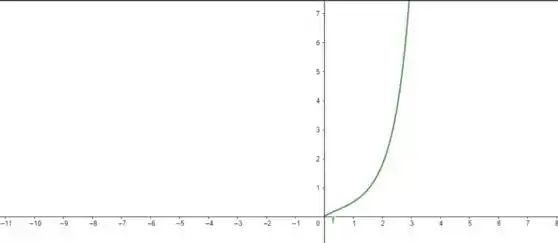
Veja que à medida que nos aproximamos de pelo lado positivo, nossa função se aproxima de 0