Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 2.6 - Ex. 49
Encontre os limites quando . Use essa informação, bem como as interseções com os eixos, para fazer um esboço do gráfico.
Passo 1
Olá, meu querido amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
O objetivo do exercício é calcular o limite de uma função dada conforme tende para o infinito positivo e negativo.
A função fornecida pode ser escrita como:
Observe que quando é um número muito grande e positivo, o fator se torna muito grande e positivo, enquanto se torna negativo e, portanto, muito pequeno.
Isso significa que a função se torna um número muito grande e negativo quando se aproxima do infinito positivo, ou seja:
Da mesma forma, a análise pode ser feita para se aproximando do infinito negativo, resultando em:
Passo 2
Agora, considere o caso em que é muito negativo. Nesse caso, o fator se torna muito grande e positivo, enquanto o fator se torna muito negativo.
Isso significa que a função se torna muito negativa quando se aproxima do negativo infinito, ou seja:
Passo 3
Agora vamos calcular os interceptos da função fornecida.
O intercepto ocorre quando .
Para encontrar o intercepto , vamos substituir na função fornecida.
Assim, obtemos o intercepto da função fornecida em .
Passo 4
Agora, observe que o intercepto da função ocorre quando .
Para encontrar o intercepto , resolvemos para .
Portanto, a função tem interceptos em , e .
Agora, observe que o intercepto da função ocorre quando .
Para encontrar o intercepto , resolvemos para .
Portanto, a função tem interceptos em , e .
Passo 5
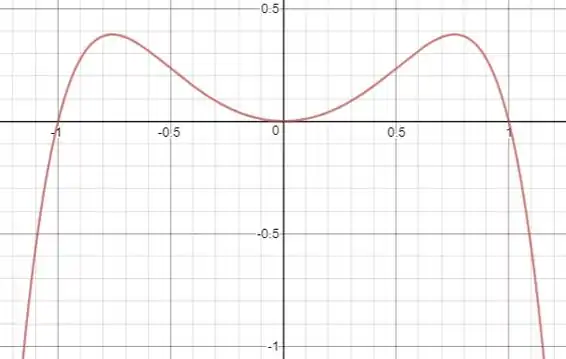
Usando essa informação, vamos esboçar a função fornecida.
A função cruza o eixo nos interceptos , ou seja, em e , e cruza o eixo no intercepto , que é em .
A função se aproxima de tanto da esquerda quanto da direita de , então mantenha o gráfico para baixo para grandes e positivos e negativos.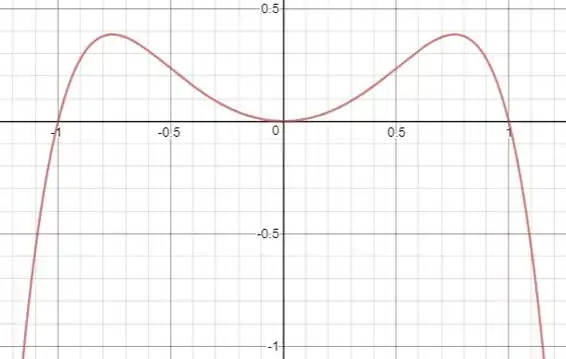
Resposta
